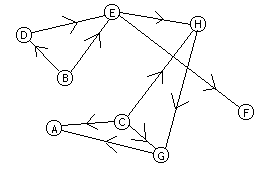
Topologisk sortering av denna graf kan ge t.ex. BDECFHGA eller CBDEHGAF
DFS-släktingar och SAT-problem
Grafteori är ju ett stort och trevligt område, så jag tänkte beskriva några algoritmer till. Jag delar upp dem i två grupper, användbara och komplicerade, det här är de användbara hoppas jag.
1. Topologisk sortering
Vi börjar med något enkelt. Lite av detta togs upp på Spelteori men det förtjänar en egen beskrivning. Problemet uppkommer t.ex. då man har en massa saker att göra, men för att kunna göra en viss sak kanske man måste ha gjort ett antal andra saker innan, och frågan är i vilken ordning man ska göra sakerna. Eller om man ser det grafteoretiskt, givet en riktad, acyklisk graf (DAG), ordna noderna i en rad så att alla bågar går från vänster till höger.

Topologisk sortering av denna graf kan ge t.ex. BDECFHGA eller CBDEHGAF
Oftast räcker det med denna intuitiva lösning:
Spara hur många bågar A[v] som leder in till varje nod, d.v.s.
ingraden för varje nod.
repeat
Välj en nod v med A[v] = 0.
För varje båge från v till en annan
nod u, minska A[u] med 1.
until alla valda
Att det alltid finns en nod v med A[v] = 0 följer av att grafen
är och förblir acyklisk under hela processen. Om A-värdena
helt enkelt sparas i en array som söks igenom varje gång blir
komplexiteten O(V^2). Om man dessutom använder en kö för
att lägga 0-noderna i blir den O(E), vilket är optimalt.
Men å andra sidan kan följande O(E)-algoritm vara enklare
att skriva:
Kör DFS
på grafen och låt en "tidsräknare" öka med 1 varje
gång en ny nod hittas. Spara för varje nod räknarens värde
(sluttid) när noden lämnas, d.v.s. när du har sökt
igenom allting nedanför noden och backtrackar för att gå
tillbaka uppåt. Om noderna sorteras efter minskande sluttid så
är detta en topologisk sortering. Beviset finns i Introduction to Algorithms
(CLRS). I praktiken behöver man inte spara sluttiden utan man kan direkt
placera noderna baklänges i en resultat-array allteftersom de är
färdigbehandlade.
Med DFS menas här att man försöker starta rekursionen
från alla möjliga noder (i valfri ordning), men att man aldrig
besöker en nod som man redan har varit på. Räknaren ska
alltså inte nollställas när en ny rekursion påbörjas.
Anledningen att man måste starta från varje nod är att
man inte kan förutsätta att alla noder går att nå
var man än börjar. Detsamma kan också gälla i en oriktad
graf om denna inte är sammanhängande, och då ger
en sådan här multistarts-DFS de olika sammanhängande komponenterna
i grafen, en för varje påbörjad rekursion.
2. Strongly connected components
I en sammanhängande komponent i en oriktad graf finns det minst en väg mellan varje par av noder. Man inför nu något liknande i en riktad graf, nämligen starkt sammanhängande komponenter , men kravet är nu att det mellan varje par av noder finns vägar i båda riktningarna. Exempel ges i figuren nedan.
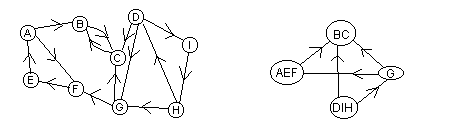
En riktad graf (t.v.) och dess starkt sammanhängande komponenter
i komponentgraf en (t.h.)
Att ta fram de starkt sammanhängande komponenterna kan precis som
topologisk sortering göras på flera sätt. Jag skriver här
den lite magiska algoritm som ges i CLRS.
Uppdelningen i starkt sammanhängande koponenter kan ibland användas som en del av en annan algoritm. I vissa problem kan man nämligen strunta i hur bågarna går inuti en komponent och bara intressera sig för bågarna som går mellan olika komponenter. Dessa bågar tillsammans med komponenterna som noder bildar en ny, mindre graf, den s.k. komponentgrafen. Notera att komponentgrafen är acyklisk per definition.
Ett problem där uppdelningen kan vara användbar är 2-SAT. För att förklara detta måste jag först göra en kort utvikning och förklara vad det allmäna satisfierbarhetsproblemet SAT innebär.
3. Satisfierbarhetsproblem (SAT)
Antag att du har n booleanska variabler som var och en kan ha värdet sant eller falskt. Du får nu en logisk formel innehållande variablerna samt NOT (!), AND, OR och paranteser. Den fråga du ska besvara är om det är möjligt att tilldela variablerna sådana värden så att hela formeln blir satisfierad (d.v.s. får värdet sant). T.ex. är formeln
(x AND y) AND (!x OR !z) AND (z OR !y OR x)
satisfierbar eftersom du kan sätta x=sant, y=sant och z=falskt. Däremot
är formeln
(x OR y) AND z AND (!z OR (!x AND !y))
inte satisfierbar. Det visar sig att problemet är NP-komplett,
d.v.s. det finns antagligen inget sätt att lösa problemet som
är fundamentalt bättre än att testa alla olika tilldelningar.
Med hjälp av logik kan man visa att hur formeln än ser ut så
går det att skriva en helt ekvivalent formel som har formen
(A11 OR A12 OR A13) AND (A21
OR A22 OR A23) AND .... AND (Ak1 OR A
k2 OR Ak3)
d.v.s. k paranteser åtdskilda med AND, vardera innehållande
3 literals åtskilda med OR, där varje literal
kan vara antingen en variabel x, y .. eller en negerad variabel
!x, !y ...Denna form kallas 3-CNF och problemet att kontrollera
satisfierbarhet kan vi kalla 3-SAT. Eftersom varje formel kan skrivas i
3-CNF, måste naturligtvis även 3-SAT vara NP-komplett (annars
skulle vi kunna lösa SAT polynomiskt genom att gå över till
3-CNF).
3-SAT är ett mycket väl studerat problem. Bl.a. kan man visa att om man gör en randomiserad algoritm som helt enkelt utgår från en slumpmässig tilldelning och sedan upprepande 3n gånger väljer en slumpmässig variabel i en parantes som inte är satisifierad och ändrar dess värde, och efter dessa 3n gånger börjar om med en ny tilldelning (Schöning's algoritm) så blir den förväntade exekveringstiden O(1,333^n) vilket är mycket bättre än den naiva sökningen som har O(2^n). Dessutom finns det naturligtvis många algoritmer som i praktiken är bättre. Dock är skillnaderna såpass små att 3-SAT är ganska ointressant som tävlingsuppgift.
Om vi däremot begränsar oss till 2 literals i varje parantes,
så blir problemet plötsligt lösligt på linjär
tid, O(n+k). Ett typexempel på detta problem, 2-SAT, är
Excursion från BOI 2001, där varje person mostavarar en parantes
och varje stad en variabel. 2-SAT kan lösas på olika sätt,
t.ex. ger en sorts matchningsalgoritm rätt svar. Men det effektivaste
och snyggaste är följande:
Tävlingsuppgifter
| Problem | Tävlingens hemsida | Hjälp och kommentarer |
| Excursion | BOI 2001 | |
| Network of Schools | IOI
1996
|
|
|
Manhattan
|
SM 2000
|
|
| Rare Order
XOR Following Orders
|
Problem Set Archive | |