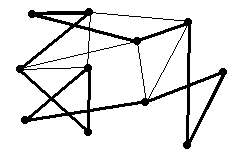
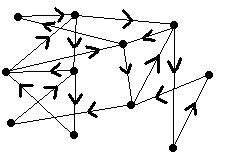
Hamiltonkrets
Problem: Givet en sammanhängande oriktad graf, bestäm om
det finns en cykel som innehåller varje nod exakt en gång.
Eulerkrets
Problem: Givet en sammanhängande oriktad graf, bestäm om
det finns en cykel som innehåller varje båge exakt en gång.

|

|
|
|
|
Även om dessa två problem kan verka snarlika, har de helt olika lösningar.
1. Hamiltonkrets
Det finns troligen inget sätt att lösa problemet på polynomisk tid.
Med detta menas att man inte har lyckats skriva ett program som
avgör om det finns en Hamiltonkrets i en godtycklig graf och som har
en exekveringstid proportionell mot n^p, där n är antalet noder
och p en konstant som ändå tillåts vara hur stor som helst.
Naturligtvis kan man skriva ett rekursivt program som letar igenom alla tänkbara
vägar att gå, men då blir exekveringstiden exponentiell,
alltså proportionell mot p^n istället, och dessa funktioner växer
otroligt mycket snabbare när antalet noder blir stort. Man har dock
inte ännu lyckats bevisa att problemet inte går att lösa
(polynomiskt). Problemet tillhör en grupp som kallas NP-kompletta problem,
och man har visat att om ett av dem är lösbart så är
alla de andra också lösbara.
En
lista med några NP-kompletta problem (från Algorithm design manual)
2. Eulerkrets
En Eulerkrets existerar om och endast om alla noder har jämn grad.
Beviset för detta ges lämpligen genom en metod för att konstruera en Eulerkrets. Eftersom alla noder har en grad som är ett jämnt tal finns inga "lösa ändar", alltså måste det finnas minst en cykel i grafen. Börja med att hitta en cykel, och ta sedan bort de bågar som ingår i cykeln. Då försvinner två bågar från varje nod i cykeln, men eftersom två är ett jämnt tal kommer den kvarvarande grafen fortfarande att uppfylla jämngradskriteriet. Därför kan man hitta en ny cykel och ta bort den på samma sätt. Processen fortsätter tills alla noder har graden 0 så att inga bågar finns kvar. Då har man fått ett antal cykler som inte har någon båge gemensam, men som har gemensamma noder där de kan "kopplas ihop". Börja gå runt i en cykel tills du kommer till en sådan skärningsnod. Där går du ett varv i den andra cykeln istället innan du fortsätter i den första. Om du råkar stöta på ytterligare en skärningsnod medan du går runt i den andra cykeln, tar du ett varv runt denna tredje cykel o.s.v. Proceduren utförs lämpligen rekursivt. Eftersom grafen var sammanhängande från början, kommer du att ha gått runt alla cyklerna innan du kommer tillbaka till startpunkten. Om algoritmen implementeras på ett smart sätt är den linjär med avseende på antalet bågar, vilket gör att även stora grafer klaras lätt.
Övningsuppgift
Skriv ett program som utför denna algoritm och testa den på den
här grafen. INDATA
Första raden innehåller antalet noder (1000) och bågar (7185),
sedan en rad för varje båge med numren på de två noder
bågen förbinder. Noderna är numrerade 0..999. Maxgraden är
20.
Varianter
Man kan, istället för att leta efter en sluten krets, försöka finna vägar med olika start- och slutnoder. Hamiltonproblemet förblir då lika svårt och Eulers lika lätt, men kravet blir istället att alla noder ska ha jämn grad utom start- och slutnoden som ska ha udda. Man kan också definiera båda problemen på riktade grafer. En Eulerkrets existerar då om alla noder har samma ingrad som utgrad.
En vanlig variant på Hamiltonkretsen uppstår om grafen är viktad och man vill minimera viktsumman för de bågar man väljer. Detta klassiska problem kallas handelsresandeproblemet eftersom det ofta handlar om att minimera den vägsträcka man färdas då man besöker ett antal bestämda platser. Om man förutsätter att resandet går att göra fågelvägen, kan man naturligtvis också helt enkelt få koordinaterna för platserna. Detta motsvarar en komplett graf där vikten av varje båge är lika med avståndet mellan platserna (Pythagoras sats). Tyvärr är dessa problem också NP-kompletta, så om man har stora grafer får man lita till heuristiska metoder . Dessa fungerar oftast bättre på den sista, geometriska versionen av problemet eftersom man då kan använda sig av t.ex. triangelolikheten.
En variant på Eulerkretsen är det kinesiska brevbärarproblemet. Där ska man också minimera viktsumman, men man måste passera varje båge minst en gång. En Eulerkrets skulle naturligtvis vara perfekt, men om inte alla noder har jämn grad får man hitta någon annan metod. Om man kunde lägga till bågar mellan de noder som har udda grad, skulle man få en Eulergraf. Men brevbäraren måste naturligtvis fortfarande följa de bågar som finns, så vikten av de nya bågarna blir helt enkelt den kortaste vägen mellan noderna i ursprungsgrafen. Om det finns många uddagradsnoder gäller det att bestämma vilka par som ska förbindas för att summan av vikterna ska bli så liten som möjligt, och detta är inte helt enkelt. Med en modifierad flödesalgoritm går det åtminstone att göra det hela polynomiskt, så inte heller brevbärarproblemet är NP-komplett.
Tävlingsproblem
Jag förmodar att inga alltför avancerade algoritmer behövs
för dessa problem.
| Problem | Tävlingens hemsida | Hjälp och kommentarer |
| The Postal Worker Rings Once (117) | Problem Set Archive | |
| John's trip (302) | Problem Set Archive |