Föreläsning 4: Klasser, konstruktorer, länkade listor och rekursion
Klasser
Med klasser kan man kapsla in data och funktioner som hör ihop.
Metoden __init __ är en specialmetod som kallas konstruktor. Det är
den som anropas när man skapar en klass. T.ex.
class Nod:
def __init__(self, s):
self.something = s
x = Nod("lite av varje")
print x.something
Alla interna metoder (kallas ofta medlemsfunktioner eller enbart
metoder) tar som extra parameter
self. Det är
self
håller reda på vilket objekt man skapar.
Funktioner i en klass anropas med genom att använda punkt. Exempel i
lab 2 finns t.ex en dictionary som anropar medlemsfunktionen has_key
todo.has_key('check')
Funktionen has_key måste veta vilken dictionary den ska
titta. Variablen todo måste skickas med i anropet. Hur görs det? Jo,
alla medlemsfunktioner (metoder) i en klass tar en extra parameter
self som pekar på objektet man pekar på.
Länkade listor
En länkad lista består av ett antal objekt, noder som är sammanlänkade
genom att varje nod refererar till nästa nod. Dessa referenser kallas
ofta next-pekare. Klassen Node skulle kunna användas för att skapa en
länkad lista med heltal.
class Node:
data = None
next = None
def __init__(self, d, p):
self.data = d
self.next = p
Listan kan vi skapa med följande rader:
p = Node(13, None)
p.next = Node(15, None)
p = Node (4, p)
Vilket ger följande lista
p -> [ 4 ] -> [ 13 ] -> [ 15 ] -> None
Man kan göra bort sig och tappa bort noder, t.ex. om vi sätter
p.next.next = None efter koden ovan så är det inget som
håller i noden med talet
15. Denna nod kommer att städas undan av pythons skräphanterare
(garbage collector)
Rita instanser
Att kunna rita instanser är väldigt viktigt när man försöker förstå
kod. I moderna utvecklingsmiljöer finns avlusare (debuggers) som kan
visa minnet när man stegar igenom ett program men det kan aldrig
ersätta okunskap av att rita minnesbilder.
Rita en låda för varje variabel. Rita klassinstanser som en låda som
innehåller flera lådor, ett för varje fält. Var noga med att namnge
fälten korrekt. Exempel för den länkade listan:

Träd
Om man lägger till en till pekare i Nod klassen kan man spänna upp ett en trädstruktur. Nedan följer två exempel.
class TreeNode:
def __init__(self, d, p, d):
self.data = d
self.next = p
self.down = d
|
|
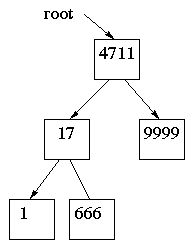
class Treenode:
def __init__(self, d):
self.data = d
self.left = None
self.right = None
|
|
Om trädet är sorterat kan man söka i det väldigt snabbt.
Rekursion
Rekursion är ett sätt att lösa problem som går ut på att man skriver en metod som anropar sig själv.
- Rekursiv tanke: reducerar problemet till ett enklare problem med samma struktur
- Basfall: det måste finnas ett fall som inte leder till rekursivt anrop
Sifferexempel
Fråga: Hur många siffror har heltalet n?
Rekursivt svar: En siffra mer än om man stryker sista siffran i n, ...men tal mindre än tio är ensiffriga.
def NoOfDigits(n):
if n < 10: return 1 # Basfall
else: return 1 + NoOfDigits(n/10) # Rekursivt anrop
Fråga: Vilken siffersumma har heltalet n?
Rekursivt svar: Sista siffran plus siffersumman om man stryker sista siffran i n, ...men noll har siffersumman noll.
def SumOfDigits(n):
if (n==0): return 0 # Basfall
return (n%10) + SumOfDigits(n/10) # Rekursivt anrop
Fråga: Hur skriver man talet n binärt?
Rekursivt svar: Först skriver man n/2 (heltalsdivision) binärt och sen skriver man en nolla eller etta beroende på om n var jämnt eller udda. Avbryt då tal är 0 eller 1 som skrivs ut som de är.
def WriteBinary(n):
if(n==0 or n==1): print n, # Basfall
else:
WriteBinary(n/2) # Rekursivt anrop
print n % 2,
Listexempel
Vi tänker oss en länkad lista av objekt, där varje objekt innehåller
ett tal och en next-pekare. Den representerar en kö och variabeln
first pekar på den första posten.
Fråga: Hur lägger vi till en post i kön
Om listan inte är tom försöker vi stoppa in ett element i den lista
som vår next-pekare pekar på. I basfallet är listan tom. Då returnerar
vi en ny post. Observera att vi måste ta hand om returvärdet i det
rekursiva anropet.
def insert(p, value) :
if (p == None): return Node(value)
else: p.next = insert(p.next, value)
return p
När fungerar det dåligt?
Det finns fall där en rekursiv lösning inte lämpar sig. Ett exempel är
Fibonaccitalen. Leonardo Fibonacci skrev år 1225 en bok där han
beskrev denna intressanta talföljd: Sista december föds en kaninpojke
och en kaninflicka. Vid två månaders ålder och varje månad därefter
producerar varje kaninpar ett nytt kaninpar.
#Månad 0 (nov) 1 (dec) 2 (jan) 3 (feb) 4 (mar) 5 (apr) 6 (maj) 7 (jun) 8 (jul) 9 (aug)
#Kaninpar 0 1 1 2 3 5 8 13 21 34
def fib(n) :
if (n <= 1): return n # Basfall
else: return fib(n-1) + fib(n-2) # Rekursivt anrop
Om man ritar upp anropskedjan ser man att många delträd räknas ut
flera gånger. För att räkna ut fib(5) så måste vi räkna ut fib(4) och
fib(3). När vi räknar ut fib(4) kommer vi att ånyo räkna ut fib(3).
Antal anrop kan uppskattas med följande resonemang. Antal operationer
för att räkna ut fib(n) = fib(n-1) + fib(n - 2) >= 2f(n - 2) Alltså
fib(n) >= 2f(n - 2) >= 4f(n - 4) >= 8f(n - 8) >= 16f(n - 16) Att
halvera så här kan man göra n/2 gånger och får =
Om man använder två extra variabler för att spara redan beräknade
värden kan man ta en for-slinga istället för rekursion vilket går i
linjär tid, O(n).
def fib_iter(n) :
f0=0
f1=1
f2=1
for i in xrange(1, n):
f2=f1+f0
f0=f1
f1=f2
return f2
Rekursivt basfall eller avbrottsvillkor
Att komma på en rekursiv tanke kan vara klurigt och skojigt. En del
fokuserar då på vad är basfallet. För
NoOfDigits skulle det
kunna vara när vi bara har en siffra. Den rekursiva tanken blir, jag
räknar en siffra och skickar vidare resten av siffrorna rekursivt.
def NoOfDigits(n):
if n < 10:
return 1 # Basfall
else: return 1 + NoOfDigits(n/10) # Rekursivt tanke: 1 + resten
Andra föredrar att tänka på rekursion som ett rekursivt anrop (man
anropar sig själv) och att det måste finnas ett avbrottsvillkor så att
man inte håller på i evighet.
def NoOfDigits(n):
if n < 10: # Avbrottsvillkor
return 1
else: return 1 + NoOfDigits(n/10) # Rekursivt anrop
Det kan finnas olika basfall/avbrottsvillkor. T.ex. istället för att
avbryta vid sista siffran så avbryter vi när vi inte har någon siffra:
def NoOfDigits(n):
if n == 0: # Avbrottsvillkor
return 0 # Basfall
else: return 1 + NoOfDigits(n/10)
Hur fungerar det?
När man skriver egna rekursiva metoder bör man lita på att det
rekursiva anropet fungerar - man behöver inte analysera anropsgången
för varje fall. Men för att förstå varför rekursion kan vara extra
minneskrävande är det vara bra att känna till hur Java (och andra
programspråk) hanterar rekursiva anrop.
- För varje anrop skapas en aktiveringspost som innehåller data för anropet, t ex parametrar, lokala variabler och anropspunkt.
- Aktiveringsposten pushas på en stack.
- När det rekursiva anropet är klart poppas aktiveringsposten från stacken, varefter föregående anrop ligger överst på stacken.
NoOfDigits (1)
NoOfDigits (10)
NoOfDigits (106)
NoOfDigits (1066)
Main()
Aktiveringsposterna tar extra minne i anspråk och stackhanteringen tar
extra tid, så det kan löna sig att skriva om sina rekursiva
metoder. En del kompilatorer kan optimera svansrekursiva metoder. En
metod är svansrekursiv om det rekursiva anropet står sist i
metoden. Då kan kompilatorn använda samma post i stacken i varje nytt
anrop.
Några saker att minnas
- En rekursiv metod kan alltid omformuleras utan rekursion med hjälp av en stack.
- För många problem är en rekursiv metod mycket enklare att formulera och ger kortare kod än utan rekursion. Man kan gå via den rekursiva lösningen i tanken även om man gör en icke-rekursiv lösning.
- Den rekursiva metoden kräver i regel mer minne (och tar längre tid) än motsvarande icke-rekursiva metod.


