Grafer
I den här texten introducerar vi de vanligaste begreppen inom grafteori
samt presenterar två datastrukturer för att representera grafer.
Vi ger också två grundläggande algoritmer som söker igenom
en graf på ett systematiskt sätt.
Grundbegrepp
En graf (graph) G består av två typer av element:
hörn (vertices) och kanter (edges).
Varje kant har två ändpunkter (endpoints) som båda
ligger i mängden av hörn och som förbinder (connects or joins)
de två ändpunkterna.
Hörnmängden (vertex set) för G skrivs ofta som V(G) eller
bara V om det inte finns risk för missförstånd.
En kant mellan punkerna x och y skrivs som xy.
Kantmängden (edge set) för G skrivs ofta som E(G)
eller bara E om det inte finns risk för missförstånd.
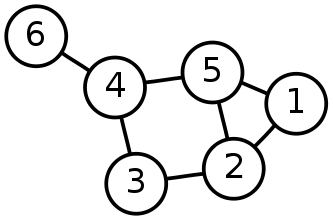
Figuren visar en enkel graf med hörnmängd V = {1, 2, 3, 4, 5, 6}
och kantmängd E = {{1,2}, {1,5}, {2,3}, {2,5}, {3,4}, {4,5}, {4,6}}.
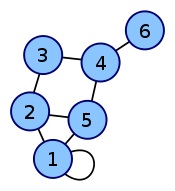
En loop är en kant vars ändpunkter är samma hörn.
En kant är multipel om det finns en annan kant med samma ändpunkter;
annars är den enkel.
En graf är enkel om den inte har några multipla kanter eller loopar
och en multigraf om den har multipla kanter.
Gradtalet för ett hörn v är antalet kanter som
har v som ändpunkt.
En väg i en graf G = (V, E) är en följd
av hörn v1, v2, ...,
vk, med egenskapen att det finns kanter
mellan vi och vi+1.
Vi säger att vägen går från v1
till vk.
Talföljden 6, 4, 5, 1, 2 är till exempel en väg från
6 till 2 i grafen ovan.
En väg är enkel om alla ingående hörn är olika.
En cykel är en väg v1, v2, ...,
vk för vilken k > 2,
de första k - 1 hörnen är olika och
v1 = vk.
Talföljden 4, 5, 2, 3, 4 är ett exempel på en cykel i grafen ovan.
En graf är sammanhängande om det för varje par av hörn
u och v finns en väg från u till v.
Om det finns en väg mellan hörn u och v så är
avståndet mellan hörnen det minimala antalet kanter på vägen
från u till v.
En sammanhängande komponent (connected component) är en subgraf i vilken varje par av hörn
är förbundna med varandra av en väg, och för vilken inga fler hörn eller
kanter kan läggas till utan att subgrafen inte längre blir sammanhängande.
Figuren visar en graf med tre sammanhängande komponenter

Träd
Ett träd är en sammanhängande enkel acyklisk graf.
Ett hörn av gradtal 1 kallas ett löv.
Riktade grafer
En riktad graf (directed graph) eller digraf (digraph)
G = (V, E) består av en hörnmängd V och en kantmängd
av ordnade par E av element i hörnmängden.
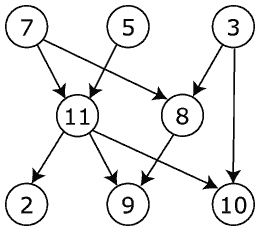
Figuren visar en enkel acyklisk digraf (ibland kallad DAG,
"directed acyclig graph") med åtta hörn och nio kanter.
Närhetsmatriser
En närhetsmatris är en enkel datastruktur för att representera
en graf G = (V, E).
Grafen representeras som en |V|x|V|-matris av heltal.
Hörnen numreras från 1 till |V| och position
(i, j) i matrisen innehåller en etta om det finns
en kant mellan i och j, annars en nolla.
Här är en graf med tillhörande närhetsmatris.
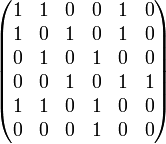
Närhetslistor
Närhetslistor är en alternativ datastruktur, med delvis
annorlunda prestanda, för grafer.
Datastrukturen består av en vektor av storlek |V|.
Position
k i vektorn består av en lista som
innehåller alla grannar till
k.
Djupetförstsökning
Djupetförstsökning DFS(g, v) är en algoritm som
besöker alla hörn i grafen g som ligger i samma komponent
som hörnet v.
// Input: graph g and vertex v.
Mark all vertices of g as not visited.
DFS(g, v)
if v is visited
return
Mark v as visited.
// Here you may perform some operation on v.
for all neighbors x of v
DFS(g, x)
Breddenförstsökning
Breddenförstsökning BFS(g, v) är en algoritm som
också besöker alla hörn i grafen g som ligger i samma komponent
som hörnet v.
Hörnen besöks i avståndsordning: först besöks hörnet v,
sedan alla grannar till v, sedan deras grannar, etc.
// Input: graph g and vertex v.
BFS(g, v)
Q = new empty queue
Mark v as visited.
Q.enqueue(v) // Add v to end of queue
while Q is not empty
a = Q.dequeue() // Remove a from top of queue.
// Here you may perform some operation on a.
for all unvisited neighbors x of a
Mark x as visited.
Q.enqueue(x)

