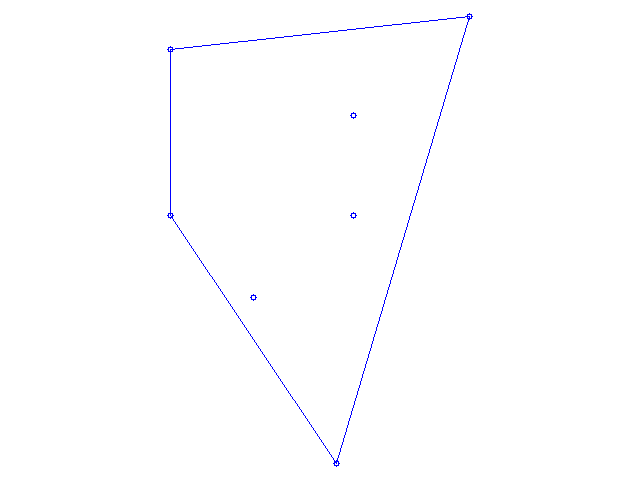
Det gäller att spänna en gummisnodd runt en punktmängd
och rita figuren. Du kommer att behöva ett par köer, ett
par stackar, en egen Point-klass och en sköldpadda.
Punkterna i
/info/grudat09/points.txt)
kan ritas så här.
from turtle import *
for line in open("points.txt"):
x,y = line.split()
x = float(x)
y = float(y)
goto(x,y)
I turtle finns bland annat anropen
up(), down(), circle(2) som
du kan använda för att lyfta och sänka pennan och för att rita
en liten cirkel. Gör det så att du får sju små cirklar.
Tillverka nu en egen klass Point med fälten x
och y och metoderna rita() och ring(). Den första ritar ett streck till punkten, den andra går
osynligt till punkten och ritar där en ring. I inläsningsslingan
skapar du Point-objekt och pushar på en stack i stället för att
rita. Sedan ska du poppa stacken och för varje punkt anropa
p.ring().
Algoritmen Graham scan börjar med att föra
över punkterna till en kö queue, alla utom punkten
längst till vänster.
Poppa först en punkt och kalla den p0. Poppa sedan
alla punkter och för över till queue, men kolla först
att dom ligger till höger om p0. Annars får punkterna
byta plats, så här enkelt.
if - - -:
p0,p = p,p0
Om dom har samma x-koordinat väljs den undre som p0.
För att se att du gjort rätt kan du tömma kön och för varje
punkt göra en ring och ett streck till p0. Det blir
en solfjäder med sex streck. Sen kommenterar du bort detta.
Algoritmen fortsätter med att ordna punkterna i kön efter
streckens lutning, nerifrån och upp. För att avgöra vilken av
punkterna p1 och p2 som ska komma först kan
man se på triangeln p0,p1,p2. Om den gås runt motsols
ska p1 vara först. Du ska definiera en funktion
def wrong(p0,p1,p2) som returnerar True om dom
går medsols och
alltså p1 och p2 bör byta plats. Ett enkelt
sätt är att beräkna kryssprodukten mellan vektorerna
(a,b)=p1-p0 och (c,d)=p2-p0, nämligen
a*d-b*c. Om den är positiv går det medsols.
För sortering behöver du en tom hjälpkö q.
Ta ut en punkt ur queue
och kalla den p2. För sedan över alla punkter till
q men kolla för varje punkt p1 att inte
def wrong(p0,p1,p2) gäller, för då ska
p1 och p2 byta plats, precis som när du
hittade vänstraste punkten. När queue är tom är
p2 den översta punkten i solfjädern och den pushar
du på stacken. Sedan kan du sätta queue=q och så är
det bara att upprepa förfarandet, alltså skapa en tom
hjälpkö, ta ut p2 osv. Iterera tills kön är tom
så ska du ha alla punkter utom p0 i stacken med
den nedersta i solfjädern överst i stacken.
För att kolla att du gjort rätt poppar du stacken och ritar solfjäder som förut. Den koden kommenteras bort sedan.
Nu behövs en till stack, hull, där punkterna i
convex hull ska hamna. Du kan genast pusha p0
på hull. Poppa p1 och pusha även den på
hull, för den måste ingå. För varje punkt p2
i stacken ska du nu kolla om p0,p1,p2 går medsols.
I så fall ska p1 kasseras, p0 pushas
tillbaka på hull och p2 pushas tillbaka
på stack. Men om det går motsols kan alla tre
punkterna pushas på hull.
Rita nu längs alla
Testa också fosterlandets konturer
Med denna labb tackar Grudat för ditt intresse och dina goda insatser.
Om du inte redan gjort webbkursvärderingen är tillfället nog inne nu!
hull-punkter, men sätt först
color("blue"). Blev det fint? Byt då punktfilen till
/info/grudat09/pentagon.txt)
och kör om programmet. Blev det något konstigt? Det beror
i så fall på att din wrong(p0,p1,p2) inte
fungerar så bra när punkterna ligger på linje, alltså då
a*d=b*c. I så fall ska det anses som wrong
när punkten p1 ligger mellan dom båda andra. Det
kan räcka att kolla att abs(a)abs(b)/info/grudat09/sweden.txt). Med många punkter är
speed("fastest") lämpligt.
Löst av ............................................hoppas.....................den.......................
Sidansvarig: <henrik@nada.kth.se>
Senast ändrad 22 november 2009
Tekniskt stöd: <webmaster@nada.kth.se>