Numerisk behandling av differentialekvationer 2 /Numerical Treatment of Differential Equations 2, 5 poäng - 7.5 ects

Aktuell omgång:/Current course: VT12, ndiff13.

Föregående omgångar:/Previous courses: VT11, ndiff11, VT12, ndiff12.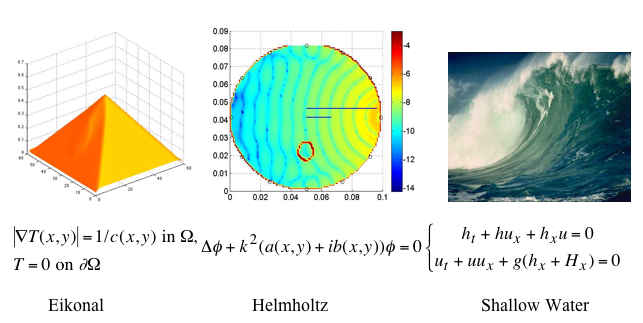

The course treats numerical methods for conservation laws and related types of partial differential equations. The pictures illustrate different types, and show, from left to right, the shortest escape times from a square with position-dependent travel speed, the wave field (acoustic or electric) in a cross section of a limb, and a breaking wave, and their mathematical models

Although linear, the Helmholtz equation is a computational challenge because it is indefinite: standard iterative schemes do not work; The other models are non-linear and have non-smooth solutions calling for special discretizations. Often one uses time-marching even for the steady problems. The course book focuses on high-resolution treatment of non-linear conservation laws, a subject which has been developed in the last twenty years.

The computer labs carry most of the credit and are relatively demanding. Efficient and clear Matlab programming is of the essence, and programming examples are provided; for the first labs, also programming technique feedback is provided.

The course treats the numerical solution of differential equations. It emphasizes partial differential equations (PDE) solved by finite difference methods and finite volume schemes. Well-posedness, stability and other properties of schemes for hyperbolic systems of equations are a major concern, as well as elliptic and parabolic equations. The choice of boundary conditions has an impact on stability and well-posedness, and will be discussed. The goal of the course is to give students

Understanding of the mathematical concepts, properties and tools for analyzing differential equations and their discretizations, and ability to carry out the manipulations and calculations required.
Working knowledge and experience of implementing FD schemes with various boundary conditions
Experience of carrying out a complete solution of a computational problem - formulation, analysis, method choice, implementation, validation, and interpretation and presentation of results.

The theoretical part introduces model equations and Fourier - Continuous as well as Discrete - techniques for the analysis of equations and schemes. The theory is complemented by a set of homework, study problems, and computer labs on the formulation, analysis, and solution of model problems from engineering science. The students are expected to have a solid background of calculus, differential equations, and linear algebra; a basic course in numerical analysis is required, as is familiarity with the NADA computer environment and MATLAB.