


Next: How is the compendium
Up: How to find the
Previous: A compendium of NP
We have chosen to structure the problems in the same way as Garey and
Johnson did [6], that is systematically in twelve
categories according to subject matter. The first five categories are
divided into subcategories. The following table shows how many problems
there are in each category in the August 1998 version of the
compendium, compared to how many there are in [6].
| Code |
Name of category |
Number
of problems in |
| |
|
G&J [6] |
compendium |
| GT |
Graph theory |
65 |
55 |
| ND |
Network design |
51 |
65 |
| SP |
Sets and partitions |
21 |
14 |
| SR |
Storage and retrieval |
36 |
10 |
| SS |
Sequencing and scheduling |
22 |
20 |
| MP |
Mathematical programming |
13 |
17 |
| AN |
Algebra and number theory |
18 |
1 |
| GP |
Games and puzzles |
15 |
2 |
| LO |
Logic |
19 |
13 |
| AL |
Automata and language theory |
21 |
5 |
| PO |
Program optimization |
10 |
2 |
| MS |
Miscellaneous |
19 |
17 |
For many categories the numbers are about the same.
This might be surprising considering that only some of the
NP-complete problems in [6] have corresponding
optimization problems. The explanation is of course that several new
NP-complete problems have been studied since 1979: an updated list
of NP-complete problems would be much larger than the original one.
It is interesting that, in some categories, there are much fewer
problems in the compendium than in [6]. The reason could
either be that there are only a few optimization problems in these
categories or that no approximability results have been shown for the
optimization problems in these classes. The latter case suggests that
more research is needed for these categories.
The current version of the compendium thus contains more than 200
problems. However, under the same basic problem, several variations
are also included. A typical entry consists of eight parts: the first
four parts are mandatory while the rest are optional.
- 1.
- The problem name that also specifies the goal of the problem.
- 2.
- The definition of the instances of the problem.
- 3.
- The definition of the feasible solutions of the problem.
- 4.
- The definition of the measure of a feasible solution.
- 5.
- A `good news' part that contains the best approximation
positive result (upper bound) for the problem.
- 6.
- A `bad news' part that contains the worst approximation negative
result (lower bound) for the problem.
- 7.
- A section of additional comments. In this section approximability
results for variations of the problem are mentioned.
- 8.
- A reference to the `closest' problem appearing in the list
published in [6].
The following is an example of what an entry looks like.
GT7. MINIMUM EDGE COLORING
INSTANCE:
- Graph
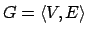 . .
- SOLUTION:
- A coloring of E, that is, a partition of E into disjoint sets
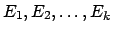 such that, for
such that, for 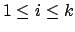 ,
no two edges in
Ei share a common endpoint in G. ,
no two edges in
Ei share a common endpoint in G.
- MEASURE:
- Cardinality of the coloring, i.e., the number of disjoint sets Ei.
- Good News:
- Approximable within 4/3, and even approximable with an absolute error
guarantee of 1 [14].
- Bad News:
- Not approximable within 4/3
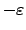 for any
for any
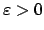 [8].
[8].
- Comment:
- Also called Minimum Chromatic Index. APX-intermediate unless
the polynomial-hierarchy collapses [4].
On multigraphs the problem is approximable within 1.1
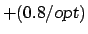 [11].
The maximization variation in which the input is extended with a
positive integer k, and the problem is to find the maximum number of
consistent vertices over all edge-colorings with k colors, is
approximable within e/(e-1) [3], but does not admit a
PTAS [12].
[11].
The maximization variation in which the input is extended with a
positive integer k, and the problem is to find the maximum number of
consistent vertices over all edge-colorings with k colors, is
approximable within e/(e-1) [3], but does not admit a
PTAS [12].
- Garey and Johnson:
- OPEN5
|



Next: How is the compendium
Up: How to find the
Previous: A compendium of NP
Viggo Kann
1998-10-31
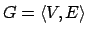 .
.
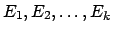 such that, for
such that, for 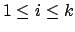 ,
no two edges in
Ei share a common endpoint in G.
,
no two edges in
Ei share a common endpoint in G.
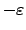 for any
for any
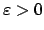 [8].
[8].
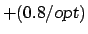 [11].
The maximization variation in which the input is extended with a
positive integer k, and the problem is to find the maximum number of
consistent vertices over all edge-colorings with k colors, is
approximable within e/(e-1) [3], but does not admit a
PTAS [12].
[11].
The maximization variation in which the input is extended with a
positive integer k, and the problem is to find the maximum number of
consistent vertices over all edge-colorings with k colors, is
approximable within e/(e-1) [3], but does not admit a
PTAS [12].