



Next: MINIMUM UNSPLITTABLE FLOW
Up: Flow Problems
Previous: MINIMUM MAXIMUM DISJOINT CONNECTING
Index
- INSTANCE:
Graph
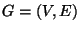 ,
length function
,
length function
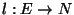 ,
set of sources
,
set of sources 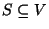 ,
sink
,
sink 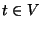 ,
demand function
,
demand function
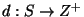 ,
finite set of cable types
where each cable type is specified by its capacity and its
cost per unit length.
,
finite set of cable types
where each cable type is specified by its capacity and its
cost per unit length.
- SOLUTION:
A network of cables in the graph, consisting of an integral number
of each cable type for each edge in G, that routes all the
demands at the sources to the sink. The demand of each source must
follow a single path from source to sink.
- MEASURE:
The total cost of building the network of cables.
- Good News:
Approximable within
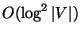 [49].
[49].
- Comment:
Variations in which there are multiple sinks (a generalization of
MINIMUM GENERALIZED STEINER
NETWORK)
or just a number k of the sources need to be connected to the sink
(a generalization of MINIMUM K-STEINER TREE)
is also approximable within
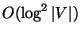 [49].
Approximable within
[49].
Approximable within 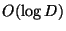 ,
where
,
where
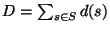 ,
for points in the Euclidean plane.
Restricted version where the network to be designed must be a two-level tree
(so that every path from a source to the sink consists of at most two edges)
is approximable within
,
for points in the Euclidean plane.
Restricted version where the network to be designed must be a two-level tree
(so that every path from a source to the sink consists of at most two edges)
is approximable within 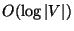 [427].
[427].




Next: MINIMUM UNSPLITTABLE FLOW
Up: Flow Problems
Previous: MINIMUM MAXIMUM DISJOINT CONNECTING
Index
Viggo Kann
2000-03-20