Comment:
Not in APX if the distances do not satisfy the triangle inequality
[250]. MINIMUM CAPACITATED K-CENTER, the variation in which the number
of vertices each center can serve is bounded by a constant L, is
approximable within 5
[318].
The converse problem, where the maximum distance from each vertex
to its center is given and the number of centers is to be minimized,
is approximable within 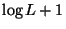 [56].
The geometric k-center problem, where the vertices lie in the plane
and the geometric metric is used, is approximable within 2, but is not
approximable within 1.822 [152].
Variants of the geometric k-center problem are also studied in the paper.
The rectilinear k-center problem, where the vertices lie in the plane
and the
[56].
The geometric k-center problem, where the vertices lie in the plane
and the geometric metric is used, is approximable within 2, but is not
approximable within 1.822 [152].
Variants of the geometric k-center problem are also studied in the paper.
The rectilinear k-center problem, where the vertices lie in the plane
and the 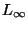 metric is used, is approximable within 2, but is not
approximable within 2
metric is used, is approximable within 2, but is not
approximable within 2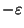 for any
for any
 [327].
If the vertices lie in
[327].
If the vertices lie in 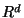 and the Euclidean or
and the Euclidean or 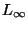 metric is used
the problem admits a PTAS whose time is exponential in k [1].
Approximable within 2 in any metric space [202].
metric is used
the problem admits a PTAS whose time is exponential in k [1].
Approximable within 2 in any metric space [202].
The vertex weighted version, where the objective is to minimize the
maximum weighted distance d(v,c)w(v), is approximable within 2
[407].
It is not approximable within 2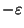 even if the distances are
induced by a planar graph of maximum degree 3 with edge lengths 1 and
vertex weights 1 [404].
MINIMUM ABSOLUTE K-CENTER, the variation in which we allow the
points in C to lie in edges (considered as curves) is also
approximable within 2 and is not approximable within
even if the distances are
induced by a planar graph of maximum degree 3 with edge lengths 1 and
vertex weights 1 [404].
MINIMUM ABSOLUTE K-CENTER, the variation in which we allow the
points in C to lie in edges (considered as curves) is also
approximable within 2 and is not approximable within
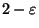 [408].
MINIMUM -ALL-NEIGHBOR K-CENTER, the variation in which we
want to minimize the distance from each vertex to
[408].
MINIMUM -ALL-NEIGHBOR K-CENTER, the variation in which we
want to minimize the distance from each vertex to 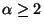 of the k
centers, is approximable within 2 when
of the k
centers, is approximable within 2 when
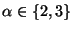 and within 3
otherwise (even for the vertex weighted version)
[311];
it is not approximable within
and within 3
otherwise (even for the vertex weighted version)
[311];
it is not approximable within 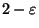 for any
for any
 [341].
The asymmetric k-center problem, where
[341].
The asymmetric k-center problem, where 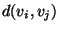 might be different from
might be different from
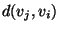 ,
is approximable within
,
is approximable within 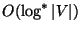 [459].
[459].
![]() even if the distances are
induced by a planar graph of maximum degree 3 with edge lengths 1 and
vertex weights 1 [404].
MINIMUM ABSOLUTE K-CENTER, the variation in which we allow the
points in C to lie in edges (considered as curves) is also
approximable within 2 and is not approximable within
even if the distances are
induced by a planar graph of maximum degree 3 with edge lengths 1 and
vertex weights 1 [404].
MINIMUM ABSOLUTE K-CENTER, the variation in which we allow the
points in C to lie in edges (considered as curves) is also
approximable within 2 and is not approximable within
![]() [408].
MINIMUM -ALL-NEIGHBOR K-CENTER, the variation in which we
want to minimize the distance from each vertex to
[408].
MINIMUM -ALL-NEIGHBOR K-CENTER, the variation in which we
want to minimize the distance from each vertex to ![]() of the k
centers, is approximable within 2 when
of the k
centers, is approximable within 2 when
![]() and within 3
otherwise (even for the vertex weighted version)
[311];
it is not approximable within
and within 3
otherwise (even for the vertex weighted version)
[311];
it is not approximable within ![]() for any
for any
![]() [341].
The asymmetric k-center problem, where
[341].
The asymmetric k-center problem, where ![]() might be different from
might be different from
![]() ,
is approximable within
,
is approximable within ![]() [459].
[459].