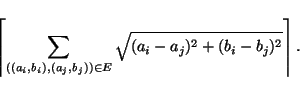
Triangulating planar graphs while minimizing the maximum degree is
approximable so that the maximum degree is bounded by ![]() for general graphs and
for general graphs and ![]() for triconnected graphs, where
for triconnected graphs, where
![]() is the degree of the graph [288].
is the degree of the graph [288].
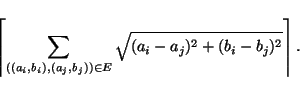
Triangulating planar graphs while minimizing the maximum degree is
approximable so that the maximum degree is bounded by ![]() for general graphs and
for general graphs and ![]() for triconnected graphs, where
for triconnected graphs, where
![]() is the degree of the graph [288].
is the degree of the graph [288].