



Next: MAXIMUM SET SPLITTING
Up: Covering, Hitting, and Splitting
Previous: MAXIMUM 3-DIMENSIONAL MATCHING
Index
- INSTANCE:
Collection C of finite sets.
- SOLUTION:
A set packing, i.e., a collection of disjoint sets
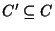 .
.
- MEASURE:
Cardinality of the set packing, i.e.,
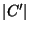 .
.
- Good News:
See MAXIMUM CLIQUE.
- Bad News:
See MAXIMUM CLIQUE.
- Comment:
Also called Maximum Hypergraph Matching.
Equivalent to MAXIMUM CLIQUE under PTAS-reduction, where
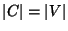 [46]. Therefore approximation algorithms and
nonapproximability results (in terms of
[46]. Therefore approximation algorithms and
nonapproximability results (in terms of 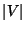 )
for MAXIMUM CLIQUE will carry over to
MAXIMUM SET PACKING.
In the weighted version of the problem the sets have positive weights and
the objective is to maximize the total weight of the sets in the set packing.
The equivalence to MAXIMUM CLIQUE holds also in the weighted case.
Approximable within
)
for MAXIMUM CLIQUE will carry over to
MAXIMUM SET PACKING.
In the weighted version of the problem the sets have positive weights and
the objective is to maximize the total weight of the sets in the set packing.
The equivalence to MAXIMUM CLIQUE holds also in the weighted case.
Approximable within 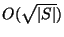 ,
where S is the
underlying base set [229]. This holds also in the weighted
case [224].
The problem MAXIMUM K-SET PACKING, the variation in which the cardinality of
all sets in C are bounded from above by a constant
,
where S is the
underlying base set [229]. This holds also in the weighted
case [224].
The problem MAXIMUM K-SET PACKING, the variation in which the cardinality of
all sets in C are bounded from above by a constant 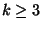 ,
is APX-complete [280], and is approximable within
,
is APX-complete [280], and is approximable within
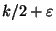 for any
for any
 [265].
The weighted version is approximable
within
[265].
The weighted version is approximable
within
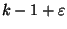 for any
for any
 [30] and within
2(k+1)/3 [98].
If the number of occurrences in C of
any element is bounded by a constant B for
[30] and within
2(k+1)/3 [98].
If the number of occurrences in C of
any element is bounded by a constant B for 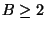 the problem is APX-complete [75] and
approximable within B, even for the weighted variation of
the problem [248].
the problem is APX-complete [75] and
approximable within B, even for the weighted variation of
the problem [248].
- Garey and Johnson: SP3




Next: MAXIMUM SET SPLITTING
Up: Covering, Hitting, and Splitting
Previous: MAXIMUM 3-DIMENSIONAL MATCHING
Index
Viggo Kann
2000-03-20