



Next: MINIMUM EXACT COVER
Up: Covering, Hitting, and Splitting
Previous: MAXIMUM SET SPLITTING
Index
- INSTANCE:
Collection C of subsets of a finite set S.
- SOLUTION:
A set cover for S, i.e., a subset
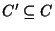 such that every
element in S belongs to at least one member of C'.
such that every
element in S belongs to at least one member of C'.
- MEASURE:
Cardinality of the set cover, i.e.,
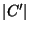 .
.
- Good News:
Approximable within
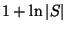 [276].
[276].
- Bad News:
Not approximable within
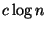 ,
for some c > 0 [423].
,
for some c > 0 [423].
- Comment:
Approximable within
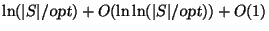 [446].
Not approximable within
[446].
Not approximable within
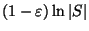 for any
for any
 ,
unless NP
,
unless NP
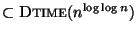 [153].
Equivalent to MINIMUM DOMINATING SET under L-reduction and equivalent to
MINIMUM HITTING SET [46].
If it is NP-hard to approximate within
[153].
Equivalent to MINIMUM DOMINATING SET under L-reduction and equivalent to
MINIMUM HITTING SET [46].
If it is NP-hard to approximate within
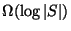 ,
then
it is complete for the class of
,
then
it is complete for the class of 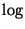 -approximable problems [305].
Approximable within
-approximable problems [305].
Approximable within 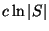 if every element of S
belongs to at least
if every element of S
belongs to at least
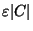 sets from C for any c>0 and
sets from C for any c>0 and
 [297] and [294].
Variation in which the subsets have positive weights and the objective is
to minimize the sum of the weights in a set cover is also approximable
within
[297] and [294].
Variation in which the subsets have positive weights and the objective is
to minimize the sum of the weights in a set cover is also approximable
within 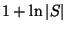 [116].
The problem MINIMUM K-SET COVER, the variation in which the cardinality of
all sets in C are bounded from above by a constant k
is APX-complete and is approximable within
[116].
The problem MINIMUM K-SET COVER, the variation in which the cardinality of
all sets in C are bounded from above by a constant k
is APX-complete and is approximable within
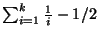 [140].
Variation in which also the number of occurrences in C of any
element is bounded by a constant
[140].
Variation in which also the number of occurrences in C of any
element is bounded by a constant 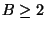 is APX-complete
[393] and approximable within B even for the general
weighted problem [61] and [246].
If, moreover, each element needs to be covered by at least K
sets with K constant, this variation is approximable within B-K+1
[398].
Approximable within 2 if the set system (S,C) is tree representable
[190].
The maximum coverage problem, where the input is extended with
an integer k and we seek to maximize the number of covered elements
using at most k sets, is approximable within e/(e-1)
[249] and not within e/(e-1) - o(1) [153].
The constrained variation in which the input is extended with a positive
integer k and a subset T of C, and the problem is to find the set
cover of size k that contains the largest number of subsets from T,
is not approximable within
is APX-complete
[393] and approximable within B even for the general
weighted problem [61] and [246].
If, moreover, each element needs to be covered by at least K
sets with K constant, this variation is approximable within B-K+1
[398].
Approximable within 2 if the set system (S,C) is tree representable
[190].
The maximum coverage problem, where the input is extended with
an integer k and we seek to maximize the number of covered elements
using at most k sets, is approximable within e/(e-1)
[249] and not within e/(e-1) - o(1) [153].
The constrained variation in which the input is extended with a positive
integer k and a subset T of C, and the problem is to find the set
cover of size k that contains the largest number of subsets from T,
is not approximable within
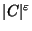 for some
for some
 [476].
Variation in which a distance matrix between pairs of elements in S is
given and the measure of the solution is not the cardinality of the cover
but its diameter (i.e., the maximum distance of any pair of elements in
C') is not approximable within any constant in the general case. If the
distance matrix satisfies the triangle inequality then this variation can
be approximated within 2 and no better approximation is possible. Similar
results hold if the cover can be partitioned into clusters and the goal is
to minimize the maximum diameter over all clusters [28] (see
also MINIMUM K-CLUSTERING).
[476].
Variation in which a distance matrix between pairs of elements in S is
given and the measure of the solution is not the cardinality of the cover
but its diameter (i.e., the maximum distance of any pair of elements in
C') is not approximable within any constant in the general case. If the
distance matrix satisfies the triangle inequality then this variation can
be approximated within 2 and no better approximation is possible. Similar
results hold if the cover can be partitioned into clusters and the goal is
to minimize the maximum diameter over all clusters [28] (see
also MINIMUM K-CLUSTERING).
- Garey and Johnson: SP5




Next: MINIMUM EXACT COVER
Up: Covering, Hitting, and Splitting
Previous: MAXIMUM SET SPLITTING
Index
Viggo Kann
2000-03-20