



Next: Weighted Set Problems
Up: Covering, Hitting, and Splitting
Previous: MINIMUM HITTING SET
Index
- INSTANCE:
Set
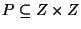 of points in the plane, a rational number r>0.
of points in the plane, a rational number r>0.
- SOLUTION:
A set of centers
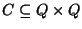 in the Euclidean plane, such
that every point in P will covered by a disk with radius r and
center in one of the points in C.
in the Euclidean plane, such
that every point in P will covered by a disk with radius r and
center in one of the points in C.
- MEASURE:
Cardinality of the disk cover, i.e.,
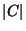 .
.
- Good News:
Admits a PTAS [251].
- Comment:
There is a PTAS also for other convex objects, e.g. squares, and in
d-dimensional Euclidean space for
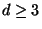 [251].
Variation in which the objective is to cover a set of points on the
line by rings of given inner radius r and width w, admits a
PTAS with time complexity exponential in r/w, for arbitrary r
and w the problem is approximable with relative error at most 1/2
[252].
MAXIMUM GEOMETRIC SQUARE PACKING, where the objective is
to place as many squares of a given size within a region in the plane,
also admits a PTAS [251].
[251].
Variation in which the objective is to cover a set of points on the
line by rings of given inner radius r and width w, admits a
PTAS with time complexity exponential in r/w, for arbitrary r
and w the problem is approximable with relative error at most 1/2
[252].
MAXIMUM GEOMETRIC SQUARE PACKING, where the objective is
to place as many squares of a given size within a region in the plane,
also admits a PTAS [251].




Next: Weighted Set Problems
Up: Covering, Hitting, and Splitting
Previous: MINIMUM HITTING SET
Index
Viggo Kann
2000-03-20