



Next: MAXIMUM ACHROMATIC NUMBER
Up: Covering and Partitioning
Previous: MINIMUM GRAPH COLORING
Index
- INSTANCE:
Graph
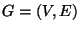 .
.
- SOLUTION:
A coloring of G, i.e., a partition of V into disjoint sets
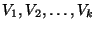 such that each
such that each 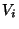 is an independent set for G.
is an independent set for G.
- MEASURE:
The sum of the coloring, i.e.
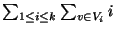 .
.
- Good News:
As easy as MAXIMUM INDEPENDENT SET[57], within a constant factor.
- Bad News:
As hard as MINIMUM GRAPH COLORING[57,156].
- Comment:
The good news hold for any hereditary class of graphs.
In particular, perfect graphs are approximable within 4 [57].
For bipartite graphs, the problem is APX-complete and approximable
within 10/9 [59]. Approximable within 2 on line graphs
[57] and on interval graphs [425].
Generalization of MINIMUM COLOR SUM where the input is extended by
positive coloring costs
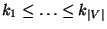 ,
and i is
changed to
,
and i is
changed to 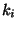 in the objective function, is not approximable within
in the objective function, is not approximable within
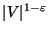 even for split, chordal, permutation and
comparability graphs. For bipartite and interval graphs, the problem
is approximable within
even for split, chordal, permutation and
comparability graphs. For bipartite and interval graphs, the problem
is approximable within 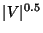 but not within
but not within
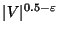 [270].
In a multicoloring generalization, we are given a graph G and an
integral color requirement x(v) for each vertex v, and are to assign
each vertex to x(v) sets
[270].
In a multicoloring generalization, we are given a graph G and an
integral color requirement x(v) for each vertex v, and are to assign
each vertex to x(v) sets 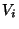 such that each
such that each 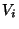 is an
independent set. The objective is to minimize
is an
independent set. The objective is to minimize
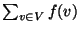 ,
where f(v) is the largest k such that v is assigned to
,
where f(v) is the largest k such that v is assigned to 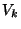 .
In the non-preemptive variant, a vertex v must be assigned to contiguous
sets
.
In the non-preemptive variant, a vertex v must be assigned to contiguous
sets
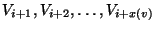 .
This variant is
approximable within
.
This variant is
approximable within 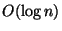 on perfect graphs, 2.796 on bipartite
graphs, and
on perfect graphs, 2.796 on bipartite
graphs, and 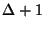 on bounded degree graphs [58],
within O(1) on interval graphs and 12 on line graphs [227],
and admits an
FPTAS on partial k-trees and a PTAS on planar graphs [226].
The preemptive variant is approximable within
on bounded degree graphs [58],
within O(1) on interval graphs and 12 on line graphs [227],
and admits an
FPTAS on partial k-trees and a PTAS on planar graphs [226].
The preemptive variant is approximable within 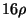 on graphs
where MAXIMUM INDEPENDENT SET is approximable within
on graphs
where MAXIMUM INDEPENDENT SET is approximable within 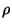 ,
within 2
on line graphs, 1.5 on bipartite graphs, and
,
within 2
on line graphs, 1.5 on bipartite graphs, and 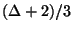 on
bounded-degree graphs [58], and admits a PTAS on trees
[228] and on partial k-trees and planar graphs [226].
on
bounded-degree graphs [58], and admits a PTAS on trees
[228] and on partial k-trees and planar graphs [226].




Next: MAXIMUM ACHROMATIC NUMBER
Up: Covering and Partitioning
Previous: MINIMUM GRAPH COLORING
Index
Viggo Kann
2000-03-20