Denna tjänst avvecklas 2026-01-19. Läs mer här (länk)

Denna tjänst avvecklas 2026-01-19. Läs mer här (länk)

SHORTEST COMMON SUPERSEQUENCE

• INSTANCE: Finite alphabet 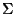$\Sigma$, finite set R of strings from 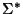$\Sigma^*$.

• SOLUTION: A string 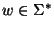$w\in\Sigma^*$ such that each string 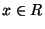$x\in R$ is a subsequence of w, i.e. one can get x by taking away letters from w.

• MEASURE: Length of the supersequence, i.e., $\vert w\vert$.

  
  

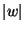• Good News: Approximable within 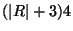$(\vert R\vert+3)4$ [169].

• Bad News: Not in APX [275].

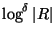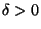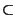• Comment: Transformation from MINIMUM FEEDBACK VERTEX SET and self-improvability. Not approximable within $\log^\delta \vert R\vert$ for some $\delta>0$ unless NP$\subset$QP [275]. APX-complete if the size of the alphabet 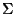$\Sigma$ is fixed [275] and [89]. Variation in which the objective is to find the longest minimal common supersequence (a supersequence that cannot be reduced to a shorter common supersequence by removing a letter) is APX-hard even over the binary alphabet, and SHORTEST MAXIMAL COMMON NON-SUPERSEQUENCE is APX-hard even over the binary alphabet [376]. Variation in which the longest common subsequence is known is also APX-hard even over the binary alphabet [133].

• Garey and Johnson: SR8