



Next: MINIMUM K-EDGE CONNECTED SUBGRAPH
Up: Cuts and Connectivity
Previous: MINIMUM QUOTIENT CUT
Index
- INSTANCE:
Graph
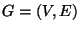 .
k is a constant,
.
k is a constant, 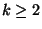 .
.
- SOLUTION:
A k-vertex connected spanning subgraph
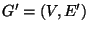 for G,
i.e. a spanning subgraph that cannot be disconnected by removing fewer
than k vertices.
for G,
i.e. a spanning subgraph that cannot be disconnected by removing fewer
than k vertices.
- MEASURE:
The cardinality of the spanning subgraph, i.e.,
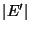 .
.
- Good News:
Approximable within 1+1/k [186] and [109].
- Comment:
On directed graphs the problem is approximable within 1.61 for k=1
[317],
and within 1+1/k for
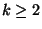 [109].
Variation in which each edge has a nonnegative weight and the
objective is to minimize the total weight of the spanning subgraph is
approximable within
[109].
Variation in which each edge has a nonnegative weight and the
objective is to minimize the total weight of the spanning subgraph is
approximable within 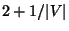 for k=2 [312]
and within 2
for k=2 [312]
and within 2
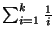 for k>2 [420].
If the weight function satisfies the triangle inequality, the problem is
approximable within 3/2 for k=2 [173] and within
for k>2 [420].
If the weight function satisfies the triangle inequality, the problem is
approximable within 3/2 for k=2 [173] and within
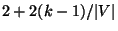 for k>2 [312].
for k>2 [312].
- Garey and Johnson: GT31
Viggo Kann
2000-03-20