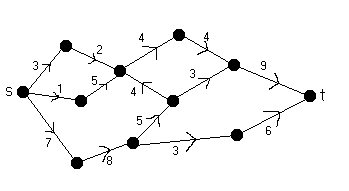
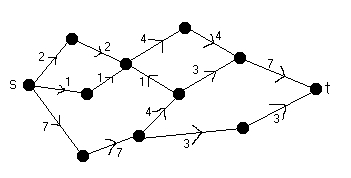
Problem: Givet en riktad graf där varje båge har en viss kapacitet, samt två noder s och t, bestäm hur stort flödet ska vara i varje båge för att man ska få så stort totalt flöde som möjligt från s till t . Regler:

• Flödet i en båge ska vara åt det håll bågen är riktad.
• Summan av flödena i de bågar som kommer in till en nod ska vara lika med summan av flödena i de bågar som går ut från noden, utom för s som saknar inflöde och t som saknar utflöde.
• Flödet i en båge får inte överstiga kapaciteten för bågen.

Given graf med kapacitet och riktning för varje båge	Maximalt flöde från s till t =10

Det är lättast att tänka sig att flödet består av vatten och att bågarna är rör med olika tjocklek, men det är bara en användning av algoritmen. Ofta handlar det istället om t.ex. nätverk av datorer. Betydligt intressantare tillämpningar tas upp i slutet av detta kapitel, t.ex. att para ihop jobb med arbetssökande. Men först gäller det att lära sig hur man löser grundproblemet.

Antag att vi i grafen har ett visst flöde, som följer reglerna ovan men inte är maximalt. För varje båge e betecknar c(e) kapaciteten för bågen och f(e) det nuvarande flödet. Vi vill hitta ett sätt att öka flödet från s till t. Om vi ökar flödet från s i någon av bågarna, säg till nod A, uppstår en obalans vid nod A. Inflödet till nod A är större än utflödet, vilket strider mot den andra regeln. Obalansen kan åtgärdas på något av följande två sätt:
1. Öka utflödet till någon annan nod B.
2. Minska inflödet från någon annan nod B.

I det första fallet leder åtgärden till att inflödet till B ökar och blir större än utflödet, varvid samma obalans uppstår vid B.
I det andra fallet leder åtgärden till att utflödet från B minskar och blir mindre än inflödet, vilket ger exakt samma situation.

Med dessa två metoder kan man skjuta problemet (obalansen) framför sig i grafen tills man kommer till t. Noden t behöver ju inte följa den andra regeln, utan när inflödet till t ökar har det totala flödet från s till t också ökat och vi har lyckats.

Det vi gör är alltså att vi hittar en väg från s till t, där varje ingående båge e antingen är

• riktad åt samma håll som vägen och inte fullt utnyttjad (forward edge). Då kan vi använda sätt 1 ovan och öka flödet genom bågen med maximalt

w(e) = c(e)-f(e).
• riktad åt motsatt håll som vägen och inte tom (backward edge). Då kan vi använda sätt 2 ovan och minska flödet genom bågen med maximalt

w(e) = f(e).

Denna sats säger oss att det räcker att från ett givet flöde (t.ex. 0) leta efter en augmenting path och sedan bearbeta flödet genom att öka flödet med w i varje forward edge samt minska flödet med w i varje backward edge. Detta upprepas tills ingen augmenting path kan hittas och vi är färdiga.

Allt detta visas lättast med ett exempel. Vid varje båge står    c / f   där c är kapaciteten och f flödet.
 
 

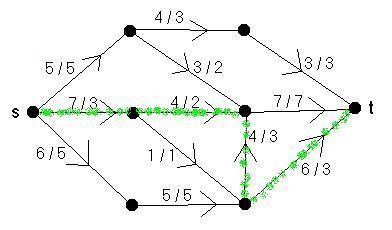
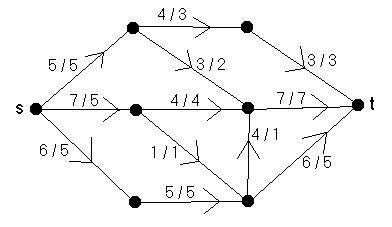
FÖRE (den gröna vägen är en augmenting path)	EFTER  (den gröna vägen har bearbetats)

Lägg märke till att w(e)-värdena för bågarna på den gröna vägen är 4, 2, 3 och 3. För hela vägen blir då w = 2. I den högra grafen går det inte att hitta en augmenting path, vilket betyder att flödet redan är maximalt.

Innan vi kan färdigställa vår algoritm återstår en sak: hur ska vi leta efter en augmenting path? Det lättaste sättet är att använda DFS . Varje nod behöver bara undersökas en gång. Det spelar nämligen ingen roll vilken kombination av forward och backward edges som leder fram till en viss nod. Det finns visserligen många utvecklade metoder för att hitta smarta augmenting paths. Med lite elaka grafer kan det nämligen bli så att varje augmenting path ökar flödet med endast 1 och om då det maximala flödet ligger på miljoner så kan det ta ett tag (utan begränsningen heltal blir det ännu värre). Dock är det absolut inget man behöver bekymra sig om på tävlingar. Har man lyckats implementera denna ganska knepiga algoritm så har man nog full poäng på den uppgiften.

Maximum_Flow(c[1..numEdges], s, t)
    f[1..numEdges] := 0             Starta utan flöde.
    repeat        Upprepa så länge det finns augmenting paths
        taken[1..numNodes] := False   Inga noder markerade
        pathLength := -1 Defaultvärde ifall ingen augmenting path hittas

        FindPath(s, 0)   Leta efter en augmenting path

        for a := 1 to pathLength do   Bearbeta den hittade vägen
            if (finns en båge e från path[a-1] till path[a]) then
                f[e] := f[e] + w      Forward edge
            else if (finns en båge e från path[a] till path[a-1]) then
                f[e] := f[e] - w      Backward edge

    until pathLength = -1

    **** f innehåller det maximala flödet ****
    SLUT
 

    ______________________________________________________________________

    FindPath(u, num, wmin)
    Den rekursiva funktion som söker efter en augmenting path.
    u = nuvarande nod,
    num = vägens längd hittills,
    wmin = minsta w[e]-värdet hittills

        taken[u] := True       Markera noden u som besökt
        path[num] := u         Lägg till u i vägen

        if node = t then
            pathLength := num    Lägg vägens längd i pathLength
            w = wmin           Lägg vägens minsta w[e]-värde i w
            return             Alla FindPath avslutas eftersom pathLength <> -1

        for e := (alla bågar från u) do
            v := (noden som e pekar till)
            if (not taken[v]) and (f[e] < c[e]) then
              En forward edge har hittats
              Rekursera från den nya noden
                FindPath(v, num + 1, min(wmin, c[e] - f[e]))
                if not pathLength = -1 then return

        for e := (alla bågar till u) do
            v := (noden som e kommer från)
            if (not taken[v]) and (f[e] > 0) then
              En backward edge har hittats
              Rekursera från den nya noden
                FindPath(v, num + 1, min(wmin, f[e]))
                if not pathLength = -1 then return
 

Maximal matchning

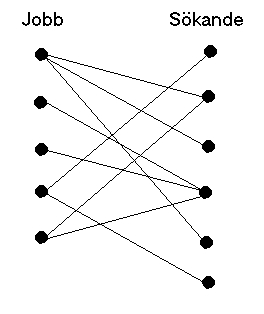
Problem: Givet ett antal jobb och ett antal arbetssökande, samt information om vilka sökande som har tillräckliga kvalifikationer för varje jobb, bestäm hur jobben ska fördelas för att så många jobb som möjligt ska tillsättas.

Exempel

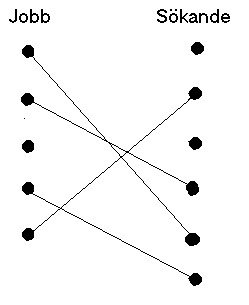
Den givna grafen (Varje båge innebär en möjlig kombination)	En maximal matchning  (4 jobb tillsatta)

Vid en första anblick är det svårt att se sambandet mellan detta problem och det förra, maximalt flöde. Men det räcker faktiskt att observera att matchningsgrafen kan göras om till en flödesgraf på följande sätt (alla bågar är riktade åt höger):

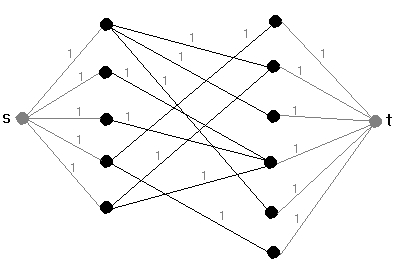
Ett sätt att lösa problemet är därför att skapa en sådan graf och sedan använda algoritmen ovan. Man behöver dock inte skapa grafen utan endast tänka sig den. Om vi bortser från de tillagda bågarna, kommer en augmenting path alltid att börja på ena sidan (låt oss säga jobb-sidan) och sedan gå i sicksack med forward edges åt höger och backward edges åt vänster, för att sluta på sökande-sidan. w kommer alltid att vara 1.

Övningsuppgift

Skriv en algoritm för matchnings-problemet.

Tävlingsuppgifter

Klarar du dessa är du duktig. Alla går att lösa med hjälp av algoritmen, men det krävs en hel del för- och efterarbete.
 

Problem	Tävlingens hemsida	Hjälp och kommentarer
Electronical plate	BOI 00	Hjälp
Rektor	SM 98	Hjälp
Telecowmunication	1996 USACO
Antenna Placement	SM 2001

Tillbaka