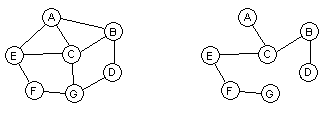
Ett uppspännande träd till en graf G, är en delgraf till G som innehåller samma noder som G men endast en delmängd av bågarna. Denna delmängd av bågar bildar ett träd som "spänner upp" grafen, se figur.

Figur 1. Till vänster en graf G, till höger ett uppspännande träd till G.
Ett självklart villkor för att ett uppspännande träd existerar för en graf G är förstås att den är sammanhängande. Om G innehåller n noder så kommer ett träd som spänner upp G bestå av n-1 bågar.
Problem: Givet en oriktad graf G, hitta det minsta uppspännande trädet (Minimal Spanning Tree, MST) till G. Med minsta menar vi att summan av vikterna på bågarna i det uppspännande trädet ska vara så liten som möjligt.
Lösningen på problemet är en förvånansvärd enkel algoritm. Låt H vara en graf med samma noder som G, men inga bågar. Vi tar nu den båge i G med minst vikt (om det finns flera bågar med samma minsta vikt väljer vi godtyckligt bland dessa), och lägger till den bågen till H. Därefter upprepas processen: vi tar en ny båge (med lägst vikt) från G och lägger till H. Om vi under denna process skapar en cykel i H, så plockar vi bort den senast placerade bågen i H.
Låt oss studera ett exempel.
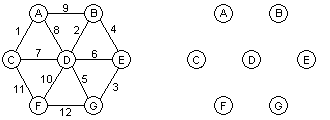
Figur 2. Till vänster en graf G som vi vill hitta ett minimalt uppspännande träd för och till höger grafen H som vi utgår ifrån vid skapandet av lösningen.
Vi börjar med att lägga till bågen AC till H eftersom den har vikten 1. Därefter kommer bågarna BD, EG och BE. Alla dessa kan läggas till utan att en cykel bildas i H. Men om vi sedan lägger till nästa båge DG, så kommer vi att ha skapat en cykel B-E-G-D-B. Alltså lägger vi inte till DG, utan går vidare till nästa båge, DE. Även denna bildar en cykel, B-E-D-B, så vi går vidare. Bågen CD kan läggas till utan problemet, och efter att ha konstaterat att AD och AB inte kan läggas till lägger vi slutligen till bågen DF, och vi har vårt minimalt uppspännande träd.
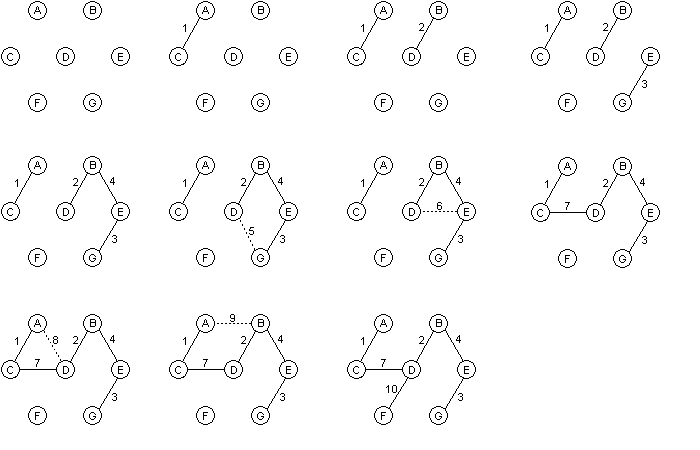
Figur 3. Båge för båge läggs till H för att skapa det minsta uppspännande trädet. De streckade bågarna är de som bildar en cykel, och läggs därför inte till.
Hur avgör man om en cykel bildas? Det finns flera sätt - ett sätt är att innan man lägger till en båge mellan två noder kollar om det finns en väg mellan dessa två noder. Det kan man ta reda på med t ex en DFS sökning. Om det finns en väg så innebär det att en cykel kommer att bildas om man lägger till en båge mellan dessa noder.
Algoritmen som beskrivits kallas för Kruskal's algoritm och är en s k "girig" algoritm (eng. "greedy") vilket betyder att den väljer den väg mot lösningen som för stunden verkar bäst. Generellt så brukar inte greedy algoritmer ge den optimala totallösningen (man får ofta backtracka och pröva andra alternativ) men i MST fallet ger den faktiskt den optimala lösningen på hela problemet.
En annan algoritm för MST är Prim's algoritm. Även den är en girig algoritm där man bygger upp trädet i en enda komponenet, genom att hela tiden lägga till den kortaste bågen från det nuvarande trädet till en nod utanför trädet. Vilken algoritm man ska välja är mest en fråga om tycke och smak, samt hur grafen G (speciellt bågarna) är givna.
Problem: I en by med ett antal hus vill man förbinda husen med en telefonledning så att det finns en förbindelse mellan samtliga hus i byn (inte nödvändigtvis en direkt förbindelse). Hur ska telefonledningen byggas för att minimera den totala längden på ledningen? Givet är husens position i xy planet.
Lösning: Vi vill hitta ett minimalt uppspännande träd mellan husen. Hörnen i grafen G motsvarar husen i byn och bågarna i G är alla potentiella ledningsvägar, dvs mellan samtliga par av hus! Grafen G är alltså en komplett graf, och vikten på bågarna är det geometriska avståndet mellan husen som motsvarar bågens ändpunkter. Efter att ha byggt upp grafen G så applicerar vi Kruskal's eller Prim's algoritm för att få fram lösningen.
| Problem | Tävlingens hemsida | Hjälp och kommentarer |
| Borg Maze | SM 2001 | Kombinerad All-Shortest-Path och MST |
| Trail
maintenance |
IOI 2003 |