Lösningsförslag tentamen 20 mars 2015
1
Det är två problem som löses. Autentisering och kryptering. Rymdvarelsen R och jordinnevånaren J har varsin uppsättning publika och privata nycklar. R signerar med sin privata nyckel och krypterar med J's publika nyckel. J autentiserar med R's publika nyckel och dekrypterar med sin privatanyckel.
2
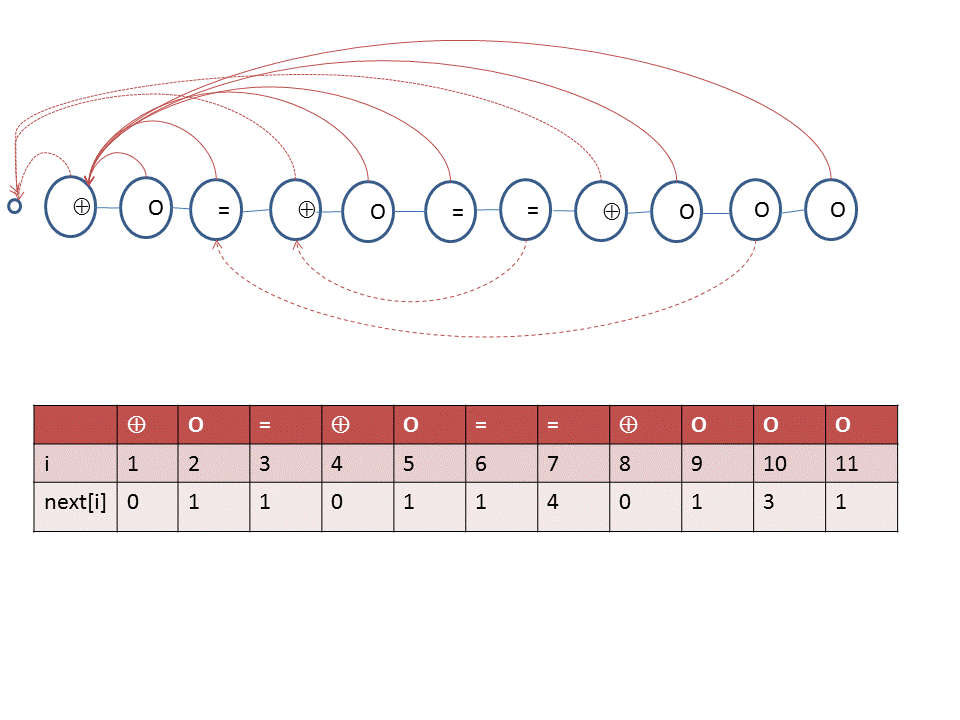
Det finns två upprepningar av inledningen. Om det testet vid det tredje =-tecknet fallerar ska man testa om det är andra plus-tecknet (plats 4). På samma sätt näst sista O-tecknet.
Sätt resterande +-tecken till 0 och övriga till 1
3
Det finns flera alternativ men det räcker att svara att bloomfilter inte har någon krockhantering på det sätt som hashvektor har. Biten skrivs över oavsett vad som stod där innan.
Ett bloomfilter har ingen krockhantering med linjär probning
Det går att argumentera för att bloomfilter har avancerad krockhantering (14 hashfunktioner med 0.514 chans av false positive). Det borde ha lämnats utrymme för att klargöra hur man tänkt och de få som skrev avancerad fick den möjligheten i efterhand.
4
Vi räknar förekomsten av de olika stjärnstorlekarna. det behövs en mellanvektor där vi lagrar resultaten. Efter att ha gått igenom och räknat tabellens stjärnor får vi en vektor
| 7 siffror | 8 siffror | 9 siffror | 10 siffror |
|---|
| 3 | 3 | 1 | 1 |
Gör om innehållet i mellanvektorn till index där stjärnorna ska lägga in. T.ex. genom att ackumulera (plussa ihop) förekomsterna.
Gå nu igenom stjärnlistan och stoppa in på den plats som anges i vektorn ovan. Den första stjärnan är 8-siffrig och hamnar på plats 6.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | Albireo 22 000 000 km |
Uppdatera mellanvektorn.
Nästa två stjärnor, en 8-siffrig och en 7-siffrig hamnar på plats 5 respektive 3. den första 8-siffriga på plats 3.
| 1 | |
| 2 | |
| 3 | Alpha Centauri A 1 500 000 km |
| 4 | |
| 5 | Aldebaran 60 000 000 km |
| 6 | Albireo 22 000 000 km |
Ett annat alternativ är att göra om mellanvektorn på följande sätt, då hamnar stjärnorna mer i ordning. Den första 7-siffriga stjärnan hamnar på plats noll.
Det är viktigt att inte slarva bort data som avståndet under räknesorteringen.
5
Redan besökta maskhål besöks om och om igen.
Man behöver hålla reda på vilka man besökt, t.ex. med en dictionary. Algoritmen behöver modifieras på två ställen.
Dels var man stoppar in ett maskhål bland de redan besökta (t.ex. efter punkt 2), dels var man kollar mot de redan besökta (t.ex. i 4a).
6
Åtkomst i vektor är O(1) och i lista O(N).
Insättning och borttagning i vektor är O(N) och i lista O(1).
7
Mars har fallit bort ur tentalydelsen vilket meddelades på tentan 45 minuter efter tentastart. Mars ska vara med.
a) och c) är de enda grammatikerna med rekursivitet. De är den enda som kan godkänna första meningen.
a) godkänner alla meningarna men underkänner inte Venus and
c) godkänner alla och underkänner Venus and
b godkänner mening 2 och 3 samt underkänner Venus and
8
Det sker onödigt många rekursiva anrop. För att räkna ut fuel(6) måste man räkna ut fuel(4) och fuel(3) flera gånger. Komplexiteten blir O(2N).
2920
2950
2970
2980
2990
2990
Bränsleåtgången minskar vilket kan tyckas konstigt men det är oväsentlig science fiction.
9
Ett oeffektivt sätt att lösa uppgiften är att gå igenom trädet i inorder och börja spara undan då första solförmörkelsen efter personens födelse påträffas och därefter spara undan alla tills första solförmörkelsen efter personens död påträffas varvid man kan sluta algoritmen. Beskriv algoritmen mer i detalj.
En annan variant är att leta sig ner i trädet. Det är viktigt att skriva en algoritm och inte bara beskriva hur den ska fungera.
Om man tänker rekursivt finns det 4 fall att ta hänsyn till:
- Om noden är None så görs ingenting (avbrottsvillkor/basfall).
- Om nodens solförmörkelse så ska den sparas undan. Båda barnen left/right ska undersökas.
- Om nodens solförmörkelse är innan personens födelse så ska enbart högerdelen av nodens delträd undersökas (anropas rekursivt).
- Om nodens solförmörkelse är efter personens dödsår så ska vänsterdelen anropas rekursivt.
Skicka med en lista i varje anrop som man kan lägga till solförmörkelser i.
10
Det behövs tre nästlade for-loopar för att gå igenom alla stjärnor och jämföra deras inbördes avstånd.
for a in stars:
for b in stars:
for c in stars:
if distance(a,b) == distance(a,c) == distance(b,c):
add_liksidig(a,b,c)
Algoritmen är O(N3). För 100000 = 105 stjärnor så blir det 1015
En annan lösning är att spara undan alla distanser. Det tar O(N2) att gå igenom alla stjärnor och ta reda på inbördes distanser. Det finns som mest N2 olika distanser. Vi kan spara undan i en distanstabell med stjärnpar och om det blir mer än två stjärnpar spara undan distansen för en senare analys. Beroende på fördelningen av stjärnavstånd skulle en sådan lösning kunna vara bättre än O(N3).

