Lösningsförslag tentamen 23 okt 2015
1
Oturstalen 3, 4, 9, 13, 17 läggs in i ett binärt sökträd. Det första talet 3 läggs in först och hamnar överst. De efterföljande talen hamnar till vänster eftersom talen är i stigande ordningsföljd. Trädet blir som en länkad lista.
3
\
4
\
5
\
9
\
13
\
17
Inorder och preorder blir samma.
3, 4, 9, 13, 17
Postorder skriver ut barnen först. Då skrivs listan baklänges.
17, 13, 9, 4, 3
Se Liangs binärträdsanimation
2
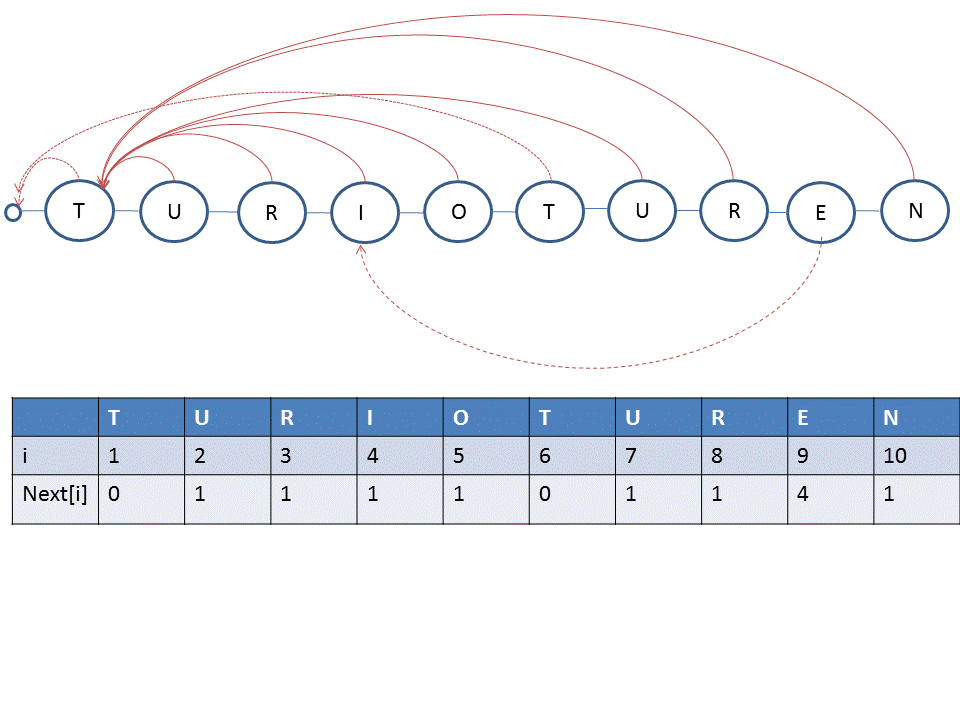
KMP-automat för TURIOTUREN
Börja med att leta upprepningar av början på ordet.
Det finns en upprepning: TURIOTUREN. Om det inte är ett E så ska man alltså testa om det är ett I d.v.s testa plats 4.
Starttillståndet backar alltid till tillstånd 0. Övriga backar här till 1.
3
Sök efter 17 i vektorn | 12 | 3 | 28 | 9 | 17 |
Binärsökningen jämför 17 med mittersta talet i vektorn, dvs 28.
Eftersom 17 är mindre än 28 sökes 17 i vänsterdelen av vektorn | 12 | 3 |. (Redan här kan man konstatera att det blir fel eftersom 17 finns i högra delen av vektorn. Det står dock i uppgiften att vi ska visa steg-för-steg vad som händer och algoritmen är inte klar.)
17 jämförs nu med det mittersta talet i vektorn | 12 | 3 | vilket är 12 (men kan vara 3 beroende på implementation). Eftersom 17 är större än 12 görs en ny sökning i högerdelen av kvarvarande vektorn (som bara innehåller siffran 3).
Då kvarvarande vektor är tom rapporteras att talet 17 inte finns i vektorn.
Felet beror på att vektorn inte är sorterad. Binärsökning förutsätter en sorterad vektor!
4
Vid breddenförstsökning är det lämpligt att använda en kö
Vid djupetförstsökning är det lämpligt att använda en stack
Vid bästaförstsökning är det lämpligt att använda en prioritetskö
5
Värsta fallet uppträder när pivotelementet väljs så att uppdelningen efter partitionering blir maximalt skev. Exempelvis om en vektor redan är sorterad samt att det yttersta elementet väljs som pivotelement.
Efter partitionering så ska alla element förutom pivotelementet sorteras. I detta fall sker aldrig någon halvering av antalet element som ska sorteras.
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
6
se en svart katt OK
gå under på golvet NEJ
lägga salt på vägen OK
7
För fembokstaviga ord är len(s) = 5. Hashfunktionen h(s) = 2 * len(s)%10 = 2 * 5 % 10 = 10 % 10 = 0
för alla fem orden
Med linjär probning kommer orden att ligga efter varandra
| 0 | prova |
| 1 | kliva |
| 2 | ramla |
| 3 | gråta |
| 4 | snyta |
Orden ligger klustrade i vektorn. Enbokstaviga h(1)=2 och tvåbokstaviga h(2)=4 ord kommer att krocka och bidra till klustringen. Det är lite klurigt att ta bort ett element, man måste skilja på en tom plats och en plats som varit upptagen.
Med kvadratisk probning hamnar de första orden
| 0 | prova |
| 1 | |
| 2 | |
| 3 | |
| 4 | ramla |
| 5 | kliva |
Det tredje ordet kommer att "slå runt", vektorn är bara tio stor, och hamna på plats 4 (14%10). Det 4:e ordet probas först till plats 0 (30%10) men där är det upptaget, därefter plats 5 (55 % 10) där det också är upptaget. Enligt uppgiften behöver vi inte proba vidare med värden utanför givna tabellen (55+36 = 91 -> plats 1).
Klustringen är inte like påtaglig som med linjär probning. Enbokstaviga ord krockar inte längre. Tvåbokstaviga ord krockar men probningen är inte densamma som ordet det krockar med. Det är fortfarande lika klurigt att ta bort element.
8
Det finns fler än tre aspekter. Här är några förslag:
- Att använda xor är snabbt. Mycket snabbare än RSA.
- xor-nyckeln är en engångsnycker och behöver genereras om för varje meddelande. RSA nycklarna behöver inte genereras om.
- Engångsnycklarna måste distribueras på ett säkert sätt. Den publika RSA nyckeln är lättare att distribuera eftersom den innehållet inte är hemligt.
- xor-nyckeln garanterar inte autentisering, om någon kommit över nyckeln kan man skicka ett falskt meddelande (men endast ett ty engångsnyckel). RSA medger både autentisering och kryptering.
9
Ett första försök
Vi börjar med en algoritm som kollar kön (men förstör den).
- Plocka ut två element ur kön, a och b.
- Börja därefter en loop tills kön är tom.
- Plocka ut ett element ur kön, c, och kontrollera att elementet är summan av de två föregående.
- Spara de två föregående elementen b och c inför nästa jämförelse.
Koden blir ungefär som följer:
a = q.dequeue()
b = q.dequeue()
while (! q.isEmpty()):
c = q.dequeue()
if c != a + b:
print("TURTAL HITTAD")
break
else:
a = b
b = c
Men för att inte förstöra kön så måste vi sätta tillbaka elementen i kön. Gör det efter varje dequeue-anrop. Vi behöver dessutom komma ihåg första element (first = a) och ändra slingan till while c != first.
Slutlig algoritm
- Plocka ut ett element ur kön, a, med dequeue
- Spara första elementet, first = a
- Stoppa tillbaka a i kön med enqueue
- Plocka ut ett element ur kön, b, med dequeue
- Börja därefter en loop:
- Plocka ut ett element ur kön, c,
- Bryt loopen om c == first (då har vi gått ett helt varv)
- Annars: Kontrollera att c är summan av de två föregående (a och b)
- Spara de två föregående elementen b och c inför nästa jämförelse.
10
Vi ska konstruera en algoritm för att lägga till så få bitar som möjligt till kodorden, så att Hammingavståndet för kodorden blir d.
Vilken typ av problem är det här?
Vi kan modifiera kodorden på olika sätt och får då en massa olika förslag på koduppsättningar.
Grafproblem - startnoden är den ursprungliga koduppsättningen, ett steg bort i grafen
har vi noder där koduppsättningen modifierats med en bit.
Vi söker en koduppsättning som uppfyller ett visst villkor, men inte vilken som helst. Så få
bitar som möjligt ska läggas till. Det här går att göra med breddenförstsökning!
Vi låter en nod innehålla en hel uppsättning med n stycken m-bitars kodord.
Ett exempel på en koduppsättning för n=3 och m=4 är:
1001
1101
1111
Barnen skapas genom att vi gör alla möjliga förlängningar med en bit. Här
är barnen på första nivån för exemplet ovan:
|
10010
11010
11110
|
10010
11010
11111
|
10010
11011
11110
|
10010
11011
11111
|
10011
11010
11110
|
10011
11010
11111
|
10010
11011
11111
|
10011
11011
11111
|
För att se till att vi får med alla kombinationer
på ett strukturerat sätt har vi lagt till de binära talen 000, 001, 010, 011 osv.
Algoritm:
- Skapa en lista
bin med de binära talen från 0 upp till 2n-1.
- Skapa en tom kö.
- Skapa ursprungsnoden. Den ska innehålla en lista
koder med de n ursprungliga kodorden.
- Lägg ursprungsnoden i kön.
- Upprepa följande tills Hamming(koder) == d, eller kön är tom:
- Ta ut första noden ur kön.
- Gå igenom listan
bin. För varje binärt tal:
- Skapa en ny nod genom att lägga till de binära siffrorna till
koder
- Lägg in den nya noden i kön.
Datastrukturer:
- Noder med en lista
koder där aktuella uppsättningen kodord lagras.
- Inga föräldra-pekare. Om vi hittar en nod som uppfyller kravet Hamming(koder) == d
så är
koder lösningen.
- Ingen dumbarnstruktur. Algoritmen ger inga identiska noder som behöver sållas bort.
