Föreläsning 4: Binära sökträd och binära tal

Allmänna träd
Binära träd
Rekursiva tankar för binärträd
Binära sökträd
Binära tal

Allmänna träd

Stack och kö är två viktiga datastrukturer man kan bygga av objekt, där varje objekt refererar till ett annat objekt.

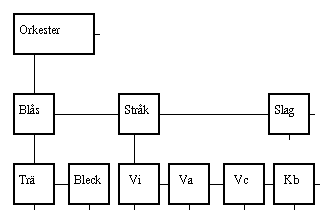TRÄD Med två referenser i varje objekt kan man emellertid bygga mer intressanta träd, till exempel ett som beskriver en symfoniorkesters sammansättning.
Här har objekten följande utseende.

   class Node:
     value=""  
     down=None
     right=None

All systematisk uppdelning kan beskrivas med liknande träd, till exempel ett bokverks uppdelning i delar, kapitel, sektioner osv. Man kan också tänka sej det som ett släktträd och då kallas ofta down-referensen för firstChild och rightreferensen för nextSibling. Det är ganska förvånande att det räcker med två referenser i varje objekt, oavsett hur stora barnaskarorna är.

Binärträd

När man talar om binärträd brukar man tänka på en lite annorlunda bild. Ett binärträd är en länkad struktur med ett värde och två pekare i varje nod.

class Node:
  value=None
  left=None
  right=None

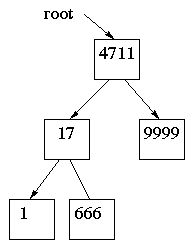
Utifrån når man trädet genom variabeln root som pekar på den översta noden (datalogiska träd har roten uppåt). Rotnodens vänsterpekare pekar på ett mindre binärträd och högerpekaren på ett annat mindre binärträd. Och det konstaterandet kan ses som en rekursiv definition av begreppet binärträd!

Antalet nivåer i trädet avgör hur många objekt det kan innehålla. Ett fullt träd med k nivåer innehåller 2 höjt till k objekt minus 1. Exempel: k=3 i vår bild ger högst 7 objekt (det finns plats för två till under 9999). Man kan också säga att ett balanserat träd med N objekt har cirka log N nivåer.

Rekursiva tankar för binärträd

Fråga: Hur många noder finns i binärträdet?
Rekursivt svar: En nod mer än i vänsterträdet och högerträdet tillsammans ...men ett tomt träd har noll noder.

    def antal(p):
      if p is None: return 0
      return 1+antal(p.left)+antal(p.right)

Anropet antal(root) ger nu rätt svar!

Om man ska skriva ut alla talen i trädet vill man oftast göra det i så kallad inordning (eng. inorder), dvs från vänster till höger.
Fråga: Hur skriver man ut trädet i inordning?
Rekursivt svar: Först skriver man ut vänsterträdet, sedan rottalet, sist högerträdet.
...men ett tomt träd skriver man inte alls.
Följande funktion gör att write(root) skriver ut 1 17 666 4711 9999 för vårt träd.

#Inordning
   def write(p):
     if p is None: return
     write(p.left)
     print p.value
     write(p.right)

Om man kastar om dom tre sista satserna får man ändå ut alla talen på skärmen men i andra ordningar. Preordning (eng. preorder) innebär att rottalet skrivs först, sedan vänsterträdet och sist högerträdet. I vårt exempel blir ordningen 4711 17 1 666 9999.

Om vi återgår till orkesterträdet kan vi se att preordning faktiskt ger vettigare utskrift. Så här blir koden i det fallet.

#Preordning     
   def write(p):
     if p is None: return
     print p.value
     write(p.down)
     write(p.right)

Utskriften blir då den naturliga. Om vi för tydlighets skull använder indragning av orden på lägre nivå blir utskriften

  Orkester              
    Blås
      Trä
      Bleck
    Stråk
      Vi
      Va
      Vc
      Kb
    Slag

(Hur gör man för att få dessa indragningar?)

Slutligen kan man skriva ut i postordning (eng. postorder) och det innebär att vänsterträdet skrivs först, sedan högerträdet och sist roten. Det ger 1 666 17 9999 4711 i vårt exempel.

Binära sökträd

I vårt exempelträd ligger små tal till vänster och stora tal till höger. När det är på det sättet har man ett binärt sökträd, så kallat eftersom det går så snabbt att söka reda på ett objekt i trädet. Låt oss säga att vi söker efter 666. Vår algoritm blir följande

Kolla först rottalet.
Om talet är 666 har vi funnit vad vi söker.
Om talet är större än 666 letar vi vidare efter 666 i vänsterträdet.
Om det är mindre än 666 letar vi vidare i högerträdet.
...men om vi når en None-referens finns inte 666 i sökträdet.

Sökningen kan implementeras rekursivt om man låter anropet finns(p,value) returnera True ifall ordet finns i det delträd där p är rot.

def finns(p,value):
    if p is None: return False
    if value==p.value: return True
    if value<p.value: return finns(p.left,value)
    if value>p.value: return finns(p.right,value)

Men den kan också göras utan rekursion. Tidskomplexiteten blir densamma.

def finns(p,value):
    while True:
        if p is None: return False
        if value==p.value: return True
        if value<p.value: p=p.left
        if value>p.value: p=p.right

Det här är ju nästan precis samma sak som binär sökning i en vektor. I båda fallen blir antalet jämförelser cirka log N, men vektorn har två nackdelar.

Insättning av nytt objekt i vektorn kräver att man flyttar i genomsnitt N/2 gamla objekt. I binärträdet flyttar man aldrig noder.
Trädet kan bli hur stort som helst men vektorns storlek ges i dess deklaration (om det är en sammanhängande följd av minnesceller).

Ett problem med binärträd är att dom kan bli obalanserade, och då försvinner den snabba sökningen. Ett riktigt obalanserat sökträd med dom fem talen i exemplet har 1 i roten, 17 till höger, 666 till höger om det osv. Det blir bara en så kallad tarm. I vissa fall har binärträd en tendens att bli obalanserade med tiden, till exempel när nyfödda förs in i ett träd sorterat på personnummer och då alltid hamnar längst till höger. Ett annat problem är att det är mycket svårt att ta bort en nod mitt inne i trädet. Ofta avstår man från det.

Abstrakta sökträd

Nu tänker vi oss att binärträdet har implementerats i en egen fil bintree.py och vi vill använda det som en abstrakt ordlista. För en abstrakt ordlista bör åtminstone tre anrop finnas: exists, put och write.

from bintree import Bintree

wordlist=Bintree()            # Skapar ett trädobjekt
 - - -          
  if wordlist.exists(word):...# Returnerar True om ordet finns i trädet 
  wordlist.put(word)          # Sorterar in ett nytt ord i trädet
  wordlist.write()            # Skriver ut alla ord i bokstavsordning

Endast dessa tre metoder kan anropas utifrån. Men om man vill implementera metoderna rekursivt måste man kunna göra anrop av typen finns(p,value) och därför definierar man ytterligare tre metoder i filen bintree.py, men ovanför klassen Bintree. Den metod som anropas, wordlist.exists(word), innehåller bara en sats.

  def exists(self,value):
        return finns(self.root,value)

Den låter alltså finns göra jobbet. Varför kan då inte huvudprogrammet direkt göra anropet if finns(wordlist.root,word)? Det skulle ju strida mot abstraktionen - det är inte meningen att någon utomstående ens ska känna till att det finns en root!

Svårast att implementera är insättningen. Man skulle tro att satsen
putta(self.root,newvalue)
skulle kunna skicka vidare jobbet till en rekursiv metod putta, men det går inte. När trädet är tomt är rotpekaren None, men när den första noden sätts in ska rotpekaren peka på den. Men self.root kan bara ändras inifrån objektet, så därför får man skriva så här.

    def put(self,newvalue):
        self.root=putta(self.root,newvalue)

Anropet till putta returnerar en pekare till det nya trädet och den läggs in i self.root. Men det är bara första gången som tilldelningen behövs. Så här blir principen för putta.

def putta(p,newvalue):
    if p is None:                       # Skapa en ny nod med det nya
      - - -                             # värdet och returnera den
    if newvalue<p.value:                
        p.left=putta(p.left,newvalue)   # Rekursiv inputtning
    elif newvalue>p.value:
        p.right=putta(p.right,newvalue)
    else:                               # Värdet fanns redan i trädet!
      - - -                             
    return p                            # Returnera pekare till det
                                        # modifierade trädet

Hur ska trädet reagera om det användare vill lägga in redan finns där? Ett sätt är att alltid spara bara det senaste eller första av de inlagda sakerna med samma värde (vi väljer detta i labben). Beskriver man tydligt sin lösning så i dokumentationen så fungerar det bra.

Dessutom kan ju användaren hela tiden använda exists-funktionen för att kontrollera om det den har för avsikt att lägga till redan finns i trädet...

Sökträd med information

Det är sällan man nöjer sej med att veta att en söknyckel (som kan vara textsträng eller tal) finns i databasen; oftast vill man att sökningen ska ge tillbaka information om det sökta. I varje trädnod måste det då finnas adressen till ett objekt som innehåller informationen.

   class Node:
       key=""              # Det som man sorterar på
       info=None           # Informationen om key
       left=None
       right=None

Sökmetoden getInfo(key) blir likadan som exists men returnerar p.info i stället för True/False.

Obalanserade träd

Det finns många sätt att göra om ett obalanserat träd till ett balanserat. Till exempel kan man spara hela trädet i en (sorterad) array och skapa trädet på nytt genom att ta elementen i lämplig ordning. Att göra om hela trädet tar O(n) varje gång. Bättre är att se till att trädet är balanserat efter varje insättning. Ett sätt att göra det är röd-svarta träd där man ger varje nod en extra egenskap (röd eller svart) och ställer upp regler för hur noderna ska vara ordnade. Om reglerna tillämpas varje gång man lägger till eller plockar bort en nod så hålls trädet balanserat.

Användningsområden

Trädstrukturer är hierarkiska och sådana datastrukturer är mycket vanliga. Några exempel:

Filsystemet använder träd (man kan ha underkataloger i underkataloger).
En kompilator skapar ett syntaxträd för programmet.
Databaser använder träd (snabb sökning).
Schackprogram använder träd för att gå igenom resultaten av möjliga drag.
Vid datakomprimering kan man använda träd för att få fram en optimal kod (Huffmanträd, kommer på komprimeringsföreläsningen).

Binära tal (och andra baser)

Till vardags använder vi decimala talsystemet med tio siffror: 0-9. Andra talsystem finns, t ex binära tal (två siffror: 0-1), oktala tal (åtta siffror: 0-7) och hexadecimala tal (sexton siffror:0-F).

Decimalt	Binärt	Oktalt	Hexadecimalt
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13
20	10100	24	14

Fråga: Hur skriver man talet n binärt?
Rekursivt svar: Först skriver man n/2 (heltalsdivision) binärt och sen skriver man en nolla eller etta beroende på om n var jämnt eller udda, ...men talen 0 och 1 skrivs likadant binärt.

def writebinary(n):
    if n==0 or n==1:
        print n,
    else:
        writebinary(n//2)
        print n%2,