Föreläsning 6: Hashning

Idén med hashning
Komplexiteten för sökning
Dimensionering av hashtabellen
Hashfunktionen
Krockhantering
Klassen Hashtable
Pythons dictionaries
Användningsaspekter
Språkteknologi

Stavningskontroll: Boolesk hashtabell, Bloomfilter
Informationssökning: Sökmotorer, Google

Idén med hashning

Binärsökning i en ordnad vektor går visserligen snabbt, men sökning i en hashtabell är oöverträffat snabbt. Och ändå är tabellen helt oordnad (hash betyder ju hackmat, röra). Låt oss säga att vi söker efter Lyckan i en hashtabell av längd 10000. Då räknar vi först fram hashfunktionen för ordet Lyckan och det ger detta resultat.

   hash("Lyckan") -> 1076540772

Hashvärdets rest vid division med 10000 beräknas nu

   1076540772 % 10000 -> 772

och när vi kollar hashtabellens index 772 hittar vi Lyckan just där!

Hur kan detta vara möjligt? Ja, det är inte så konstigt egentligen. När Lyckan skulle läggas in i hashtabellen gjordes samma beräkning och det är därför hon lagts in just på 772. Hur hashfunktionen räknar fram sitt stora tal spelar just ingen roll. Huvudsaken är att det går fort, så att inte den tid man vinner på inbesparade jämförelser äts upp av beräkningstiden för hashfunktionen.

Komplexiteten för sökning

Linjär sökning i en oordnad vektor av längd N tar i genomsnitt N/2 jämförelser, binär sökning i en ordnad vektor log N men hashning går direkt på målet och kräver bara drygt en jämförelse. Varför drygt? Det beror på att man aldrig helt kan undvika krockar, där två olika namn hamnar på samma index.

Dimensionering av hashtabellen

Ju större hashtabell man har, desto mindre blir risken för krockar. En tumregel är att man bör ha femtio procents luft i vektorn. Då kommer krockarna att bli få. En annan regel är att tabellstorleken bör vara ett primtal. Då minskar också krockrisken, som vi ska se nedan.

Hashfunktionen

Oftast gäller det först att räkna om en string till ett stort tal. Datorn gör ingen skillnad på en bokstav och dess nummer i ASCII-alfabetet, därför kan ABC uppfattas som 656667. Det man då gör är att multiplicera den första bokstaven med 10000, den andra med 100, den tredje med 1 och slutligen addera talen. På liknande sätt gör metoden


hash(key)

men den använder 32 i stället för 100. För en binär dator är det nämligen mycket enklare att multiplicera med 32 än med 100. Här är en förenklad variant:

def hash2(s):           # Returns a hashcode for this string, computed as 
  result = 0            # s[0]*32^[n-1] + s[1]*32^[n-2] + ... + s[n-1]
  for c in s:                    # where n is the length of the string, 
    result = result*32 + ord(c)  # and ^ indicates exponentiation. 
  return result

Om man vill söka på datum eller personnummer kan man använda det som stort heltal utan särskild hashfunktion. Exempel: sexsiffriga datum kan hashas in i hashvektorn med 031202 % size. En olämplig storlek är 10000, ty 031202 % 10000 -> 1202 och vi ser att endast 366 av de 10 000 platserna kommer att utnyttjas. Det säkraste sättet att undvika sådan snedfördelning är att byta 10000 mot ett närliggande primtal, till exempel 10007. Det visar sej nämligen att primtalsstorlek ger bäst spridning.

Krockhantering

Den naturliga idén är att lägga alla namn som hashar till ett visst index som en länkad krocklista. Om man har femtio procents luft i sin hashtabell blir krocklistorna i regel mycket korta. Krocklistorna bör behandlas som stackar, och hashtabellen innehåller då bara topp-pekarna till stackarna.

En annan idén är att vid krock lägga posten på första lediga plats. Är det tomt där, tittar man på nästa, osv. Detta kallas linjär probning. En fördel med denna metod är att man slipper alla pekare. En stor nackdel är att om det börjat klumpa ihop sej någonstans har klumpen en benägenhet att växa. Detta kallas för klustring.

I stället för att leta lediga platser som ligger tätt ihop kan man därför göra större hopp. Hopplängden bör då variera. Ett sätt är att "hoppa fram" i jämna kvadrater, så kallad kvadratisk probning. Om hashfunktionen gav värdet h tittar man i ordning på platserna: h+1, h+4, h+9, ... . Överstiger värdena hashtabellens storlek använder man resten vid heltalsdivision precis som vid beräkningen av h.

Ytterligare ett sätt att lösa krockproblemet är dubbelhashning. I denna variant räknas nästa värde fram med en annan hashfunktion som tar som indata den första hashfunktionens värde. För att hitta efterföljande platser låter man den andra hashfunktionen få sitt förra värde som indata.

Både kvadratisk probning och dubbelhashning ger goda prestanda om hashtabellen har femtio procent luft. En nackdel med båda metoderna är att man inte enkelt kan ta bort poster utan att förstöra hela systemet.

Klassen `Hashtable`

Hashtable är en utmärkt och lättskött klass med två anrop, put och get. Första parametern till put är söknyckeln, till exempel personens namn. Andra parametern är ett objekt med alla tänkbara data om personen. Metoden get har söknyckeln som indata och returnerar dataobjektet om nyckeln finns i hashvektorn, annars skapas ett särfall.

  from hashtable import Hashtable
  table = Hashtable()	
  table.put("one", 1)
  table.put("two", 2)
  table.put("three", 3)
  n=table.get("two")         # Nu blir n=2

Om det är risk att nyckeln inte finns skriver man så här:

  while True:
    word=raw_input("Ett engelskt räkneord:")
      try:
        print table.get(word)
      except Exception:
        print "Tyvärr okänt, försök igen!"

Klassen Hashtable finns inte inbyggd i Python. Vill man ha den får man programmera den själv. Så här skulle en del av koden för en hashtabell som använder kvadratisk probning kunna se ut:

class Node:
    # I varje position i hashtabellen lagras
    # noder med nyckel och värde
    key=""
    value=None






class Hashtable:
    size=31
    table=[None]*31
    hashiter = 0 # behövs för hashfunction() och rehash()
    
    def __init__(self,n):
        # En konstruktor. Med hjälp av denna kan man
        # vid instansiering bestämma storleken på tabellen.
        self.size=n
        self.table=[None]*n
        
    def getsize(self):
        return self.size
    
    def has_key(self,key):
        # Finns något lagrat med nyckeln "key"?
        h=self.hashfunction(key)
	p=self.table[h]
        while p!=None and p.key!=key:
            h=self.rehash(h)
            p=self.table[h]
        if p!=None and p.key==key:
            return True
        return False

    def put(self,key,value):
        # Stoppa in "value" med nyckeln "key",
        # dvs skapa en nod och stoppa in den
        # på rätt plats i "table"
        ---

    def get(self,key):
        # Hämta det som finns lagrat med nyckeln "key"
        # Om det inte finns: kasta ett särfall
        ---
        raise Exception,key+" finns inte"
    
    def hashfunction(self, key):
        # Returnera hashvärdet av key
        # "startar den kvadratiska probningen"
        ---

    def rehash(self, oldhash):
        # Beräkna nästa plats (efter oldhash)
        # enligt kvadratisk probning
        ---

Pythons dictionaries

Men man kan i stället använda Pythons inbyggda dictionaries; det är nämligen hashtabeller som bygger ut sej själv vid behov. Då kan man också indexera med hakparenteser i stället för att skriva put och get.

  tal={}               # Tomt lexikon skapas
  tal["one"] = 1
  tal["two"] = 2
  tal["three"]=3
  n=tal["two"]         # Nu blir n=2

Anropet tal.has_key("två") fungerar som förut och om man skriver tal["två"] uppstår ett särfall. (Det finns många olika typer av särfall. När ett index saknas i en dictionary kastas ett KeyError.)

Användningsaspekter

I nästan alla sammanhang där snabb sökning krävs är det hashtabeller som används. Krockar hanteras bäst med länkade listor, men i vissa programspråk är det svårt att spara länkade strukturer på fil, så därför är dubbelhashning fortfarande mycket använt i stora databaser.

I LINUX och andra UNIX-system skriver användaren namn på kommandon, program och filer och räknar med att datorn snabbt ska hitta dom. Vid inloggning byggs därför en hashtabell upp med alla sådana ord. Men under sessionens förlopp kan många nya ord tillkomma och dom läggs bara i en lista som söks linjärt. Så småningom kan det bli ganska långsamt, och då är det värt att ge kommandot rehash. Då tillverkas en ny större hashtabell där alla gamla och nya ord hashas in. Hur stor tabellen är för tillfället ger kommandot hashstat besked om.

Om man vill kunna söka dels på namn, dels på personnummer kan man ha en hashtabell för varje sökbegrepp, men det går också att ha en enda tabell. En viss person hashas då in med flera nycklar, men själva informationsposten finns alltid bara i ett exemplar. Många noder i hashtabellen kan ju peka ut samma post.

När man vill kunna skriva ut registret i bokstavsordning är hashtabellen oduglig. Binärträdet skrivs lätt ut i inordning, men är inte så bra när man vill kunna stega sej framåt och bakåt från en aktuell nod. Risken för att det ska bli obalanserat har lett till algoritmer för automatisk ombalansering av binärträd när poster läggs till och tas bort. Kända begrepp är B-träd, AVL-träd och rödsvarta träd. För femton år sedan gjordes en uppfinning som löser problemen på ett enklare sätt, nämligen skipplistan. Dessa datastrukturer ligger dock utanför denna kurs.

Språkteknologi

Hashning används i många olika sammanhang. Här betraktar vi två exempel från ämnesområdet Språkteknologi, dvs behandling av naturliga språk (mänskliga språk, till skillnad från tex programmeringsspråk) med datorer.

Språkteknologi kan delas in i sådan teknik som behandlar tal (ljudet som uppstår då vi talar) och sådan som behandlar text. Vi ska se på två exempel inom det senare.

För den som tycker det här verkar intressant finns kursen 2D1418, Språkteknologi.

Stavningskontroll

Ett stavningskontrollprogram ska läsa en text och markera alla ord som är felstavade. Om man har tillgång till en ordlista som innehåller alla riktiga svenska ord kan man använda följande enkla algoritm för att stavningskontrollera en text.

Läs in ordlistan i en lämplig datastruktur.
Öppna textfilen.
Så länge filslut inte nåtts:

Läs in nästa ord från filen.
Slå upp ordet i ordlistan och skriv ut det på skärmen om det inte finns med.

Enda problemet är hur man ska välja datastruktur för lagring av ordlistan. Svenska akademiens ordlista innehåller ungefär 200000 ord. Förutom dessa ord finns en hel del böjningsformer och oändligt många tänkbara sammansättningar. Låt oss bortse från detta och anta att vi har köpt en ordlista med dom 200000 vanligaste orden i svenskan. Om vi snabbt ska kunna stavningskontrollera en stor text med en normal persondator måste följande krav på datastrukturen vara uppfyllda.

Uppslagning måste gå jättesnabbt.
Datastrukturen får inte ta så mycket minne (helst inte ens så mycket minne som orden i klartext).
Orden måste vara kodade (eftersom ordlistan är köpt och inte får spridas till andra).
Vi kan tillåta att uppslagningen gör fel någon gång ibland.

Den sista punkten är inte ett krav utan en egenskap hos vårt problem som vi kan utnyttja. Det är nämligen inte hela världen om programmet missar något enstaka felstavat ord i en jättestor text.

Vanliga datastrukturer (sorterad array, sökträd, hashtabell) faller alla på något av kraven ovan.

Försök med datastruktur: boolesk hashtabell

Låt oss först försöka med hashning där vi inte lagrar själva orden och inte tar hand om eventuella krockar. Vi har en hashfunktion f(ord)=index som för varje ord anger en position i en boolesk hashtabell tab. Den booleska variabeln tab[f(ord)] låter vi vara sann då ord ingår i ordlistan. Detta ger en snabb, minnessnål och kodad datastruktur, men den har en stor brist: Om det råkar bli så att hashfunktionen antar samma värde för ett ord i ordlistan som för ett felstavat ord så kommer det felstavade ordet att godkännas. Om hashtabellen exempelvis är fylld till häften med ettor så är sannolikheten för att ett felstavat ord ska godkännas ungefär 50% vilket är alldeles för mycket.

Bloomfilter

Lösningen är att använda många hashfunktioner som alla ger index i samma hashtabell tab. I Viggos stavningskontrollprogram Stava används till exempel 14 olika hashfunktioner f₀(ord),f₁(ord), f₂(ord),...,f₁₃(ord). Ett ord godkänns bara om alla dessa 14 hashfunktioner samtidigt ger index till platser i tab som innehåller sant.

Uppslagning av ett ord kan då ske på följande sätt:

    for i in range(14):
       if not tab[f(i, ord)]: return False
    return True

Om hashtabellen är till hälften fylld med ettor blir sannolikheten för att ett felstavat ord godkänns så liten som (1/2)¹⁴=0.006%.

Denna datastruktur kallas bloomfilter efter en datalogiforskare vid namn Bloom. Ett abstrakt bloomfilter har bara två operationer: insert(x) som stoppar in x i datastrukturen och isIn(x) som kollar ifall x finns med i datastrukturen.

Programmet Stava kan köras på Nadas Unixdatorer med kommandot

stava filnamn

(hjälp finns via webbsidan) och stava går att köra på webben på http://www.nada.kth.se/stava/

Informationssökning

Information Retrieval (IR), informationssökning, är ett stort fält inom Språkteknologi. Den mest centrala applikationen inom IR är sökmotorn.

Sökmotorer

Sökmotorer har webbspindlar som följer alla webblänkar och tar kopior på alla webbsidor. För att snabbt hitta alla sidor som innehåller ett visst ord hashar man varje ord på varje nyinläst sida och lägger där in dels ordets textomgivning, dels skivminnesadress till den sparade websidan. Resultatet av sökning på ett visst ord är alltså en lista av webbsidor.

Sökning på flera ord ger flera listor och då visas först träffar på alla sökorden. Den inbördes ordningen mellan alla sidor beror av antalet gånger orden används i respektive text (den så kallade termfrekvensen) och hur vanligt ordet är på hela nätet (den så kallade inversa dokument frekvensen). Detta modellerar hur bra sökfrågan matchar texterna, eller omvänt hur relevanta texterna är för frågan.

Man tänker sig en gigantisk matris i vilken dokument representeras av kolumnerna. Varje rad står för ett av alla ord som finns i hela mängden dokument. I varje position i matrisen finns ett värde (ofta noll) som representerar hur väsentligt ordet antas vara för att förklara innehållet i dokumentet. Dessa värden, eller vikter, beräknas med hjälp av termfrekvensen och den inversa dokument frekvensen.

Likhet mellan två texter beräknas som skalärprodukten mellan deras kolumnrepresentationer, dvs delar de många ord blir de lika. Om man betraktar sökfrågan som en mycket kort text kan man beräkna likhet mellan den och alla texter. Sedan presenterar man texterna i likhetsordning.

Google

Det som gjort Google till ledande sökmotor är att de införde ytterligare ett sätt att mäta texters relevans. Googles upphovsmän är två studenter vid Stanford (Page och Brin) och deras geniala begrepp kallas page rank, PR. Det mäter hur "förtroendeingivande" en webbsida är. Detta mått viktas sedan ihop med likheten enligt ovan vid presentation av texterna, så att en text måste vara lik sökfrågan och ha hög page rank för att komma högt upp på träfflistan.

Idén är att en webbsida som många andra länkar till borde vara relevant. ...men det spelar väl roll hur förtroendeingivande dessa sidor är? Vi får ett cirkelresonemang, som kan uttryckas så här:

PR(p)=(1-d) + d 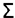_{q in B(p)} PR(q)/N_q,

där B(q) är alla sidor q som länkar till p,
N_q är antalet länkar ut från sida q
och d (0 <= d <= 1) är en dämpningsfaktor.

Formeln ger en ekvation för varje webbsida - ett jättestort linjärt ekvationssystem: x=Ax, där x är en vektor med page rank för alla sidor och A är den matris som beskriver ekvationssystemet.

Om man ansätter en ursprunlig page rank för alla webbsidor, x(0), (vilket motsvarar att man ansätter d för alla sidor i formeln ovan) kan man lösa detta ekvationssystem iterativt. Man får en bättre och bättre approximation till x så här:

x(1)=Ax(0)
x(2)=Ax(1)
x(3)=Ax(2)
osv

Följande intuition kan hjälpa för att förstå formeln för page rank: en "random surfer" följer länkar slumpmässigt från sida till sida. Med sannolikhet (1 - d) tröttnar hon och väljer slumpmässigt en annan sida bland alla andra.

Både informationssökning och stavningskontroll kan man läsa mer om i kursen 2D1418, Språkteknologi.