DD1320 Tillämpad Datalogi

Föreläsning 8: Prioritetskö, trappa (heap)

Prioritetskö

När man poppar en stack får man ut det senast inpushade. När man tar ut något ur en vanlig kö får man tvärtom ut det som legat längst tid i kön. Man skulle kunna se det som att det som stoppas in tidsstämplas och att det påstämplade talet ger prioriteten för uthämtning.

I en prioritetskö stämplas en prioritet på varje objekt som stoppas in och vid uthämtning får man objektet med högst prioritet.

En abstrakt prioritetskö kan ha föjande anrop.

put(p,x)
Stoppa in x med påstämplad prioritet p (oftast ett heltal).
x = get()
Hämta det som har högst prioritet.
isempty()
Undersök om prioritetskön är tom.
Om det man vill stoppar in i prioritetskön är ett tal kan man använda talet självt som prioritet och bara skriva put(x). Hur den då skiljer sej från en stack och från en vanlig kö ser man av följande exempel. 
      pq.put(1)
      pq.put(3)
      pq.put(2)
      x = pq.get() # x blir 3
En kö hade skickat tillbaka det först instoppade talet 1; en stack hade skickat tillbaka det senast instoppade talet, 2; prioritetskön skickar tillbaka det bästa talet, 3. I denna prioritetskö betraktar vi största talet som bäst - vi har en så kallad maxprioritetskö. Det finns förstås också minprioritetsköer, där det minsta talet betraktas som bäst.

Prioritetsköer har många användningar. Man kan tänka sej en auktion där budgivarna stoppar in sina bud i en maxprioritetskö och auktionsförrättaren efter "första, andra, tredje" gör pq.get() för att få reda på det vinnande budet. För att han ska veta vem som lagt detta bud behövs förstås båda parametrarna i pq.put(p,x). 

      pq.put(bud,person)   #person är ett objekt med budgivarens namn och bud
      winner = pq.get()    #budgivaren  med högst bud

Trappa

Den bästa implementationen av en prioritetskö är en trappa, (eng heap), som är en vektor (lista) tab tolkad som binärträd. 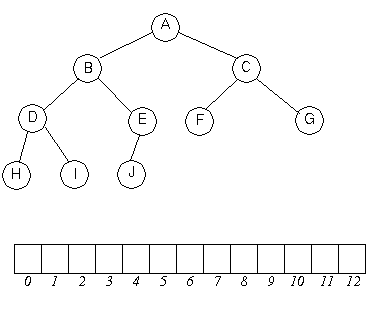HEAP Roten är tab[1] (vi använder inte tab[0], dess båda barn är tab[2] och tab[3] osv. Allmänt gäller att tab[i] har barnen tab[2*i] och tab[2*i+1]. Trappvillkoret är att föräldern är bäst, dvs varje tal ligger på två sämre tal.

Ett nytt tal läggs alltid in sist i trappan. Om trappvillkoret inte blir uppfyllt, dvs om det är större än sin förälder, byter förälder och barn plats och så fortgår det tills villkoret uppfyllts. Det här kallas upptrappning och kan i värsta fall föra det nya talet hela vägen upp till toppen, alltså tab[1].

Man plockar alltid ut det översta talet ur trappan och fyller igen tomrummet med det sista talet i trappan. Då är inte trappvillkoret uppfyllt, så man får byta talet och dess största barn. Denna nedtrappning upprepas till villkoret åter gäller.

Både put och get har komplexitet log N om trappan har N element. Nackdelen med trappan är man måste bestämma listans storlek från början.

Här följer en rudimentär implementation av en max-heap: 


class HeapNode:

    def __init__(self, value, priority):
        self.value = value
        self.priority = priority

class Heap:
    # En max-heap

    def __init__(self, maxsize):
        self.maxsize = maxsize
        self.tab = maxsize*[None]
        self.size = 0

    def isempty(self):
        return self.size  == 0

    def isfull(self):
        return self.size == self.maxsize

    def put(self, value, priority):
        if not self.isfull():
            self.size += 1
            self.tab[self.size] = HeapNode(value, priority)
            i = self.size
            while i > 1 and self.tab[i//2].priority < self.tab[i].priority:
                self.swap(i//2, i)
                i = i//2



    def get(self):
        if not self.isempty():
            data = self.tab[1]
            self.tab[1] = self.tab[self.size]
            self.size-=1
            i = 1
            while i<=self.size//2:
                mx = self.maxindex(i)
                if self.tab[i].priority < self.tab[mx].priority:
                    self.swap(i, mx)
                i = mx
            return data.value
        else:
            return None

    def maxindex(self, i):
        if 2*i+1 > self.size: return 2*i
        if self.tab[2*i] > self.tab[2*i+1]: return 2*i
        else: return 2*i+1

    def swap(self, a, b):
        temp = self.tab[a]
        self.tab[a] = self.tab[b]
        self.tab[b] = temp

Heapsort

Om man stoppar in N tal i en trappa och sedan hämtar ut dom ett efter ett får man dom sorterade. Komplexiteten för denna heapsort blir O(N log N), alltså av lika god storleksordning som quicksort. Visserligen är quicksort lite snabbare, men heapsort har inte quicksorts dåliga värstafallsbeteende. och så kan ju en heap användas till andra saker än sortering också. 
    heap = Heap(16)               
    for word in open("folksagor.txt").read().split():
        heap.put(word, word)
    while not heap.isempty():
        print heap.get()

Bästaförstsökning

Labb 4 behandlar problemet att finna kortaste vägen från FAN till GUD. Man har då ett problemträd med FAN som stamfar/urmoder, på nivån därunder barnen MAN, FIN, FAT osv, på nästa nivå fans barnbarn osv. Om man lägger barnen i en kö kommer man att gå igenom problemträdet nivå för nivå, alltså breddenförst. Om man byter kön mot en stack blir sökningen djupetförst. Med en prioritetskö får man bästaförstsökning, dvs det mest lovande barnet prioriteras och får föda barn.

Det här är exempel på en girig algoritm, där man i varje steg väljer den väg som verkar bäst för stunden, utan att reflektera över vad konsekvenserna blir i längden. Ofta ger giriga algoritmer inte den bästa lösningen, men i just det här fallet fungerar det faktiskt! Algoritmen kallas Dijkstra's algoritm (efter den holländske datalogen Edsger W. Dijkstra) och att den fungerar bevisas i fortsättningskursen DD1352 Algoritmer, datastrukturer och komplexitet.

Exempel 1: Sök billigaste transport från Teknis till Honolulu. All världens resprislistor finns tillgängliga.

Problemträdets poster innehåller en plats, ett pris och en förälderpekare. Överst i trädet står Teknis med priset noll. Barnen är alla platser man kan komma till med en transport och priset, till exempel T-centralen, 20.00. Man söker en Honolulupost i problemträdet. Med breddenförstsökning får man den resa som har så få transportsteg som möjligt.

Med bästaförstsökning får man den billigaste resan.

Exempel 2: Sök effektivaste processen för att framställa en önskad substans från en given substans. All världens kemiska reaktioner finns tillgängliga med uppgift om utbytet i procent.

Problemträdets poster innehåller substansnamn och procenttal. Överst i trädet står utgångssubstansen med procenttalet 100. Barnen är alla substanser man kan framställa med en reaktion och utbytet, till exempel C2H5OH, 96%.

Med en max-prioritetskö får man fram den effektivaste process som leder till målet.

Siluettproblemet

Om man på håll betraktar en stad i skymningen ser man inte dom enskilda byggnaderna utan bara siluetten, den yttersta konturen, avteckna sig mot himlen. Hitta på en algoritm som givet varje byggnads kontur beräknar stadssiluetten.

Anta att alla byggnader står på x-axeln, är rektangulära och beskrivs av tripplar (left, height, right) där left är vänsterväggens x-koordinat, right är högerväggens x-koordinat och height är höjden (y-koordinat).

Inmatningen består av n stycken tripplar, ordnade i stigande värden på vänsterväggar, och utmatningen ska vara en rad med x,y-koordinater som från vänster till höger beskriver siluetten. x-värdena anger var på x-axeln siluetten går vertikalt och y anger på vilken höjd siluetten fortsätter efter x-värdet. Den sista y-koordinaten är alltid noll eftersom alla byggnader står på x-axeln.

Exempel: Om n=8 och inmatningen är
(1,11,5) (2,6,7) (3,13,9) (12,7,16) (14,3,25) (19,18,22) (23,13,29) (24,4,28)
så blir utmatningen 

     x= 1  y= 11
     x= 3  y= 13
     x= 9  y= 0
     x= 12 y= 7
     x= 16 y= 3
     x= 19 y= 18
     x= 22 y= 3
     x= 23 y= 13
     x= 29 y= 0
Det här knepiga problemet kan vi lösa med hjälp av två heapar. Den ena är en min-heap, som ser till att vi får ut husväggarnas koordinater i ordning från minsta (vänstraste) till största (högraste) x-värde. Den andra är en max-heap som hjälper oss att hitta det just nu högsta huset.

Algoritm:

Programkod 

from maxheap import MaxHeap
from minheap import MinHeap

class House:
    left = None
    height = None
    right = None

    def __init__(self, left, height, right):
        self.left = left
        self.height = height
        self.right = right

def readHousesTo(xheap):
    ins = raw_input("Vilka hus finns? ").split()
    for h in ins:
        h = h.strip("()")
        hs = h.split(",")
        house = House(int(hs[0]), int(hs[1]), int(hs[2]))
        print house
        xheap.put(house, house.left)

xheap = MinHeap(20)
yheap = MaxHeap(20)

readHousesTo(xheap) # Läs in husen

x = 0
y = 0
while not xheap.isempty():
    house = xheap.get()
    if house.left > x:  # Hus med vänstervägg utplockat
        x = house.left
        if house.height > y:
            y = house.height
            print "x=", x, "y=", y
        xheap.put(House(house.left, house.height, house.right), house.right)
        yheap.put(House(house.left, house.height, house.right), house.height)

    else: # Hus med högervägg utplockat
        if house.height == y: # Det var det just nu högsta huset
            # Sök efter det hus som blir högst nu
            x = house.right
            while not yheap.isempty() and yheap.top().right <= x:
                yheap.get()     # Ta bort hus som ligger...
                                # ...till vänster om x
            if yheap.isempty():
                y = 0
            else:
                y = yheap.top().height
            print "x=", x, "y=", y