Olika former av kryptering har använts så länge man har velat ha skriftliga hemligheter. Redan dom gamla grekerna hade flera system för kryptering.
Samma effekt kan vi få genom att skriva meddelandet i en mxn-matris och bilda det kodade meddelandet genom att ta varje kolumn i texten. Den som känner till matrisens storlek kan lätt avkoda det. Man brukar skippa mellanslag och skiljetecken för att göra det svårare att knäcka koden.
JAGGÖ MMERP ENGAR NAIDE NGAML AEKENkodas alltså som:
JMENNAAMNAGEGEGIAKGRADMEÖPRELN
En variant är rot13 där man förskjuter varje bokstav 13 steg. Hamnar man utanför alfabetet roterar man runt till början igen.
def rot13(meddelande):
alfabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
kod = ""
for bokstav in meddelande:
index = (alfabet.find(bokstav) + 13) % 26
kod = kod + alfabet[index]
return kod
Om vi skippar ÅÄÖ får vi ett alfabet som består av 26 tecken,
vilket innebär att vi kan använda samma funktion för dekryptering!
rot13("HEMLIGHETER") blir URZYVTURGRE
rot13("URZYVTURGRE") blir HEMLIGHETER
Ännu hemligare blir det om vi slumpar fram en mappning
istället för att flytta fram ett visst antal steg.
ABCDEFGHIJKLMNOPQRSTUVWXY ||||||||||||||||||||||||| FSXNVDQBCULRHKTPAOMWJEIGYAlla dessa chiffer är dock enkla att knäcka om man har statistik över hur ofta varje bokstav förekommer i det aktuella språket. Så här ser det ut för svenska:
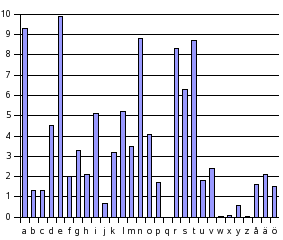
Krypteringsalgoritmen RSA (döpt efter Ron Rivest, Adi Shamir och Leonard Adleman som först publicerade den) löser detta genom att ha en offentlig nyckel och en privat nyckel. Den offentliga nyckeln delar du ut till alla, så att dom kan kryptera meddelanden och skicka till dig, men det är bara du som kan dekryptera med hjälp av den privata nyckeln.
Först måste vi beräkna nycklarna:
Sedan beräknar vi mie modulo n för att få de kodade delarna ci.
Den som vill dekryptera måste känna till d, och kan då få ut det ursprungliga meddelandet genom att beräkna cid modulo n för varje ci.
Här finns en demonstration av RSA. Prova t ex att kryptera Power Rangers hemliga kod Galwit Mysto Prifior.
För att knäcka RSA måste man faktorisera n, dvs lista ut vilka de två stora primtalen p och q är. Det finns ännu ingen algoritm som kan göra detta i polynomisk tid, dvs O(Lk) där L är längden av primtalet och k är en godtycklig konstant, vilket innebär att beräkningen tar för lång tid för att vara praktiskt användbar. Därför räknar man med att RSA i nuläget är oknäckbar för tillräckligt stora primtal.
En fortsättningskurs som bland annat handlar om tillämpningar av kryptering är DD2395 Datasäkerhet. Där får man också lära sig om t ex virus och datajuridik.
Säkerhetsaspekter tas även upp i kursen DD1334 Databasteknik som vissa av er läser redan i vår.
Vi har förstås också kursen DD2448 Kryptografins grunder (men den kräver att man läst DD1352 ADK först).
I lydelsen för labb 5 finns länk till ett testprogram:
def kontrollera(hashtabell, atomlista):
"""Kontrollerar att hashtabellen fungerar
genom att kolla att varje element i
atomlista finns"""
antal = 0
print "Testar att hitta alla atomer..."
for element in atomlista:
namn, vikt = element.split()
try:
x = hashtabell.get(namn)
if not(vikt == x or float(vikt) == x):
print namn, "har fel vikt."
else:
antal += 1
except KeyError:
print element, "fanns inte med i hashtabellen."
print antal, "element hashades korrekt."
print "Testar att hitta tio atomer som inte finns..."
knasatomer = "A o Aa cD Qz SJ pq Zz Å Åö"
fanns = 0
fannsInte = 0
for namn in knasatomer.split():
try:
x = hashtabell.get(namn)
fanns += 1
print namn, "fanns med i hashtabellen."
except KeyError:
fannsInte += 1
if fanns == 0:
print "inga knasatomer hittades."
else:
print "Av", fanns+fannsInte, "knasatomer hittades", fanns
atomlista = skapaAtomlista()
hashtabell = lagra(atomlista)
kontrollera(hashtabell, atomlista)
|