

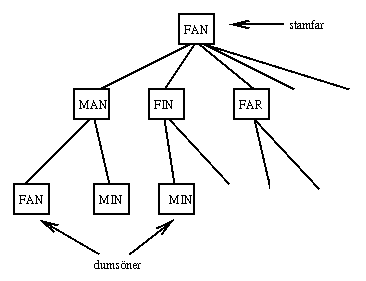
Lägg stamfadern som första och enda post i en kö. Gör sedan följande om och om igen: Plocka ut den första ur kön, skapa alla söner till denne och lägg in dom sist i kön. Första förekomsten av det sökta ordet ger kortaste lösningen.
Man kan spara in både tid och utrymme om man undviker att skapa söner som är kopior av tidigare släktingar (t ex mans son fan), så kallade dumsöner.
Breddenförstsökningsalgoritmen kan sammanfattas så här.
Breddenförstsökning ger alltid den kortaste lösningen. Ofta är det den man är ute efter. Några andra problemexempel är följande.
Vi antar att alla växlingskurser är kända, t ex 1.00 SEK -> 0.14 USD och 1.00 USD -> 7.05 SEK. En valutanod är ett belopp i en viss valuta. Vi utgår från valutanoden 1.00 SEK och låter den vara stamfar i ett problemträd. Stamfaderns söner är alla valutanoder som kan åstadkommas med en växling, till exempel 0.14 USD och 16.5 JPY. Sonen 0.14 USD har i sin tur söner, däribland 0.987 SEK. Just den är en så kallad dumson och kan lugnt glömmas bort, eftersom den är sämre än en tidigare valutanod.
Om man går igenom problemträdet nivå för nivå, dvs generation efter
generation, kanske man till sist stöter på noden 1.05 SEK.
Därmed har man funnit en lönsam växlingskedja och det är bara att sätta igång
och växla så fort som möjligt innan kurserna ändras. För att avbryta
trädgenomgången och hals över huvud återvända till huvudprogrammet kan
man generera ett särfall med
raise Exception och se till att huvudprogrammet har
try:
- - - # Om särfallet uppstår här...
except Exception:
- - - # ...teleporteras man hit
Tillsammans med särfallet kan man skicka med ett valfritt objekt, till
exempel ett meddelande, så som exemplet nedan visar.
Om man har en abstrakt kö med metoderna put, get och isempty kan breddenförstsökningen programmeras ungefär så här.
class Node # problemträdspost
amount=1.00 # belopp
currency=1 # valutanummer, SEK=1, USD=2,...
father=None # faderspekare
- - - Definition av makesons och writechain
- - - Inläsning av växlingskurserna
q = Queue()
stamfar=Node()
q.put(stamfar)
try:
while not q.isempty():
makesons(q.get()) # I makesons görs raise Exception,kedja
print "Ingen lönsam växling"
except Exception,kedja: {
print "Växla fort:",kedja
Metoden makesons skapar alla söner och lägger sist i kön.
Om man vill bli av med dumsönerna kan man ha en global vektor
best med hittills högsta belopp av varje valuta.
Ett exempel är åttadamersproblemet som innebär att man ska placera åtta damer på ett schackbräde så att ingen dam står på samma vågräta, lodräta eller diagonala linje som någon annan. Problemträdets stamfar är ett tomt bräde. Dom åtta sönerna har en dam placerad på översta raden, sonsönerna ytterligare en dam på näst översta raden etc.
Den första idén man får är ju att representera schackbrädet med
en matris. Men lösningen blir enklare om man använder en vektor,
där varje vektorelement är ett heltal som representerar damens position
på just den raden.
queen[0]=5 betyder då att damen på rad noll står i position 5.
Rekursiv tanke:
Att lösa problemet färdigt när det redan står damer på rad 0..row-1 är detsamma som...
...att för varje tillåten damplacering på rad row lösa
problemet färdigt...
... men om row=8 har man hittat en lösning.
# coding:iso-8859-1
n=8
queen=[None]*n
def completePartialSolution(row):
# Fullborda partiell lösning som har damer på rad 0..row-1
if row==n:
for r in range(n):
for col in range(n):
if queen[r]==col: print "D",
else: print "*",
print
print "==============="
return
for col in range(n):
if posOK(row,col):
queen[row]=col
completePartialSolution(row+1)
def posOK(row, col):
# Kolla om damen på rad row kan slås av damerna ovanför
for i in range(row):
if queen[i]==col: return False #rakt ovanför
if queen[i]-col==row-i: return False #snett ovanför
if col-queen[i]==row-i: return False #snett ovanför
return True
completePartialSolution(0)
Problemträdet har startpositionen som stamfar, alla positioner på ett stegs avstånd som söner och så vidare. En position som man varit på förut är en dumson.
000000010002000300040005000600070008000900100011...9999Det kräver fyrtiotusen tryckningar. Men man kan klara sej med bara tiotusentre tryckningar om man har en supersmart sekvens där varje fyrsiffrigt tal förekommer någonstans. Hur ser sekvensen ut?
Problemträdets stamfar 0000 har tio söner 00000, 00001,..., 00009, varav den förste är dumson. Breddenförst eller djupetförst? Vi vet att trädet har djupet tiotusen och att alla lösningar är lika långa, därför går djupetförst bra. Men breddenförst skulle kräva biljoner poster!
Labyrintlösning med dynamisk programmering: Skriv en nolla i startpositionen. Gå ett steg i alla riktningar och skriv en etta osv. Om man kommer till en plats som redan har besökts skriver man ingenting. Förr eller senare skriver man ett tal i målpositionen och det talet anger då kortaste avståndet från starten. Om man följer talen i avtagande ordning går man denna kortaste väg.
Partnerval med dynamisk programmering: Du står utanför ett rum med tio för dej okända personer och du måste bjuda en av dom på balen. Dom kommer ut en och en och du bedömer iskallt hur attraktiva dom är på en skala 0 - 100. Hur ser din strategi ut för att få genomsnittligt högsta utdelning?
Dden dynamiska programmeringens basfall har en enda partnerkandidat. Då år strategin klar: den partnern väljer du! Om skalan anger hur många procent av mänskligheten man överträffar, så är det klart att det förväntade talet är 50. Då lämnar vi basfallet och går över till två personer. Den första som kommer ut måste nu ha ett tal större än 50 för att vi ska slå till. Om talet är mindre än 50 chansar man förstås på att ta den sista. Med denna strategi väljs den näst sista bara om talet ligger mellan 50 och 100, och i genomsnitt är det då 75. Men i hälften av fallen tar man i stället den sista personen och kan då förvänta sej talet 50. Medelvärdet är alltså 62.5. Så här kan man fortsätta: tredjen från slutet väljer man bara om talet är större än 62.5 etc.
Påståendet att ett släppt föremål faller till marken är vetenskapligt. Varje experiment där ett släppt föremål beter sej annorlunda skulle ju falsifiera det. Men påståendet att gud skapade världen för sjutusen år sedan kan inte falsifieras. Varje fossil etc som tycks vara äldre kan ju ha skapats i dett skenbart åldrade skick. Skapelsen är alltså inte en vetenskaplig fråga.
Skulle Hitler ha segrat om han fått atombomben? Det kan man spekulera om, men vilket svar man än föreslår kan det inte falsifieras och är därför inte vetenskapligt. Vilken färg har en elektron? Har män ett kollektivt ansvar för könsdiskriminering? Vad är meningen med livet? - - - Viktiga frågor som inte vetenskapen kan besvara.