Flow simulation
Large scale simulations are used to simulate turbulent flow in many engineering applications e.g. flow over aircraft and ship hulls, flow in pipes and flow in combustion engines. The small scales of turbulence are usually modelled in these cases. By resolving all scales in direct simulation, better precision is obtained, modelling is avoided, understanding is improved and phenomena such as transition can be studied in detail. However, this will be possible only for simple geometries for the near future due to the high computational demands.
Accurate numerical methods and codes for solution of the incompressible
Navier-Stokes equations are developed in Uppsala
together with the Department of Mechanics at KTH.
The aim is to be able to simulate turbulent flow
in simple geometries on high performance computers.
Most simulations today use spectral methods in
channel-like geometries or at most second order methods in more complicated
geometries. Our flow boundaries will have curvature with the
goal to compute the flow over an aircraft wing at a Reynolds number Re of
engineering interest.
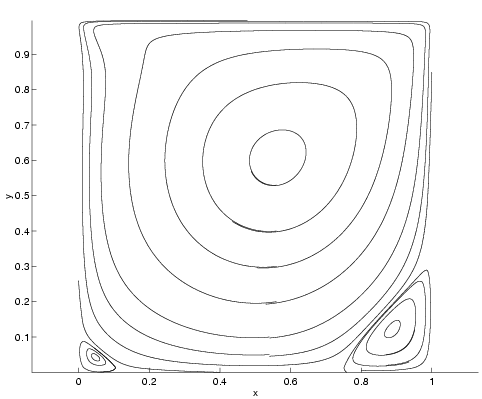 Figure 1 |
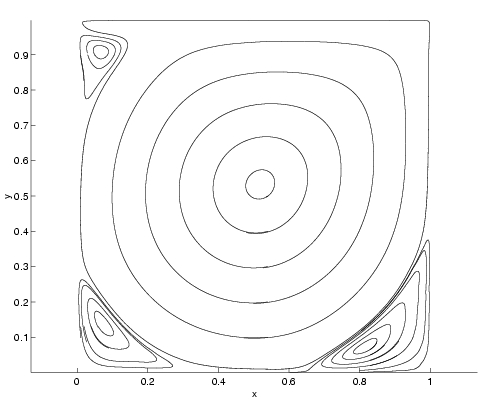 Figure 2 |
| The computed stream lines in the driven cavity problem with Reynolds number 400 in Figure 1 and 5000 in Figure 2. The flow is driven by the upper wall. No-slip boundary conditions are applied at the other walls. | |
The equations are discretized in time and space by a compact finite difference method of high order on curvilinear grids. The solution is expanded in Fourier series in the third space dimension. In each time step, a system of linear equations has to be solved coupling the velocity components and the pressure. After elimination of the velocity, the result is an implicitly defined discrete approximation of the Poisson equation satisfied by the pressure for each Fourier mode. In order to simulate high Reynolds number flow, it is crucial that the solver of the Poisson equation is robust and efficient. The equation has to be solved for, say, one hundred Fourier modes in each one of many thousands of time steps. For an example see Figures 1 and 2. An accurate and efficient solver for direct simulation is the basis for the development of subgrid models such as Large Eddy Simulation (LES), where the scales shorter than the grid size are modelled. The part of the project emphasizing the high order of accuracy in space and time of the method has been supported by the Swedish Research Council (VR).
In another project high order finite difference methods are developed for
compressible flow problems. The difference operators satisfy a summation-by-parts
(SBP) formula. Of special concern is the derivation of boundary conditions with
the SBP property. In this way accurate and stable methods have been devised and
applied to time dependent and steady state solutions of the Navier-Stokes equations.
The effect of of a high order method compared to a second order method is
illustrated below in a time-dependent problem.
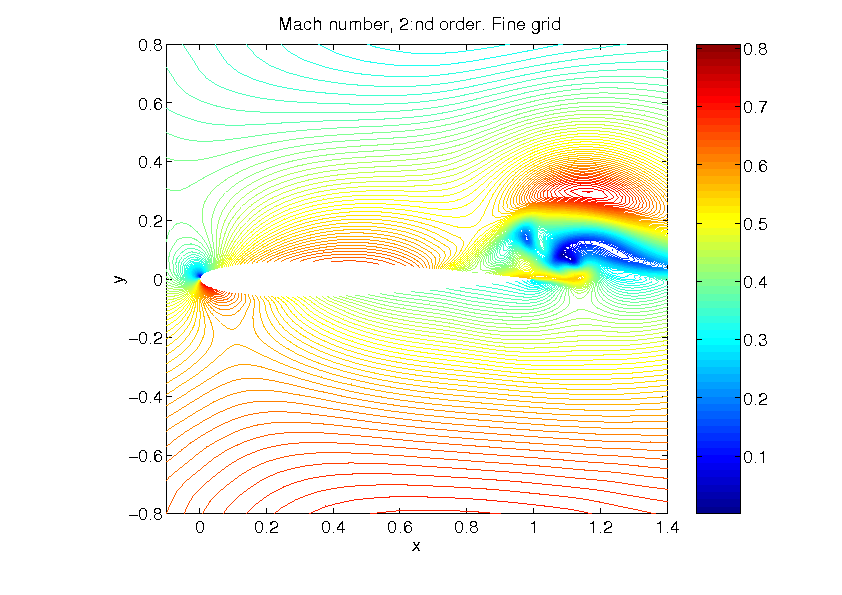
Figure 3: The interaction between a vortex and an airfoil is computed with a second order method. |
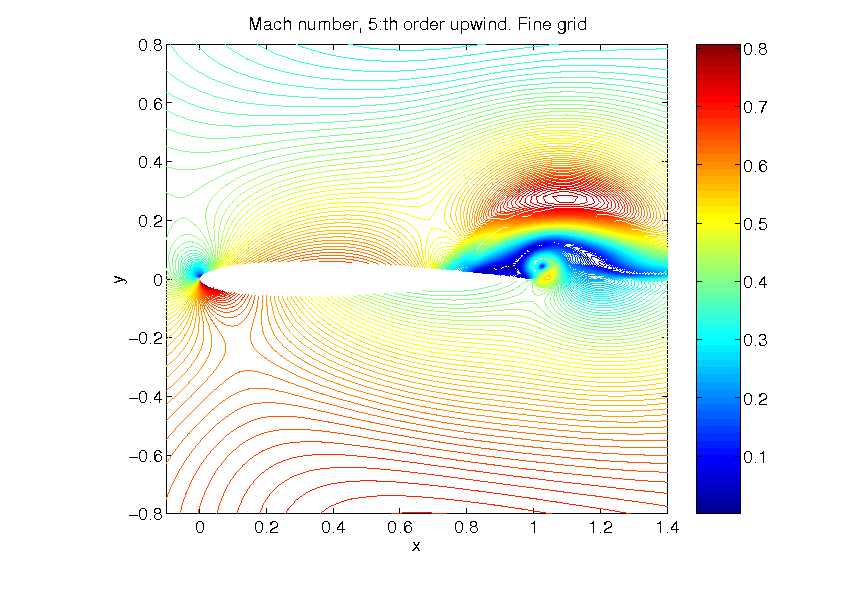
Figure 4: The interaction between a vortex and an airfoil is computed with a fifth order method. |
Past and present participants: Bertil Gustafsson, Per Lötstedt, Jan Nordström, Wendy Kress, Jonas Nilsson, Magnus Svärd, Uppsala, Dan Henningson, Arne Johansson, Arnim Brüger, Erik Stålberg, KTH.
High frequency electromagnetics
Two state-of-the-art codes for electromagnetic problems have been developed by PSCI supported by Aerotech Telub, Ericsson Microwave Systems, Saab Ericsson Space, and the Swedish Defence Research Agency (FOI). In the frequency domain, integral equations are solved using the multipole method and the approximations of physical optics. See Figure 3 for an example. A PhD thesis has been written on this subject. A hybrid method in the time domain combines the finite element method on an unstructured grid with a finite difference discretization on a Cartesian grid. The codes are now in use in the industry for prediction of e.g. radar cross section, lightning effects, and antenna performance. The time domain method has been developed further with subgrid models for wires, thin gaps and thin layers. In the frequency domain the multipole expansions have been improved and methods are available for many incident waves. The shape of the objects and the material properties have been optimized. The optimization project is performed at the Department of Electromagnetics at Chalmers in Göteborg. These projects are supported by PSCI and the Swedish Defence Material Adminstration.

Figure 5: The computed surface currents generated by an incident electromagnetic wave with 3 GHz frequency on a trainer aircraft |
The physical problems are characterized by a frequency range, and today there is a frequency gap, where no accurate and efficient simulation methods exist. Direct approximations of Maxwell's equations are possible for lower frequencies, and asymptotic techniques work well at very high frequencies. Our research will aim at closing this gap.
Higher order methods for the time dependent Maxwell equations have been
developed. The main challenges are the approximations at boundaries and
material interfaces. Recent tests with model problems show important
promise. New hierarchical methods of multipole type will also be developed
for the time dependent boundary integral formulation. These improvements
will allow for high accuracy simulations in higher frequencies with possible
coupling to the solvers based on partial differential equations.
The development of hybrid methods which use high frequency techniques in one domain to full wave equation approximations in another will then close the frequency gap for most practical problems. In this coupling a high frequency representation with rays from geometrical theory of diffraction will be combined with a wave field representation. A new technique has been developed for this numerical coupling. The technique is based on an explicit numerical translation of a solution of Helmholtz equation into a ray representation suitable as initial data to the geometrical optics equations.
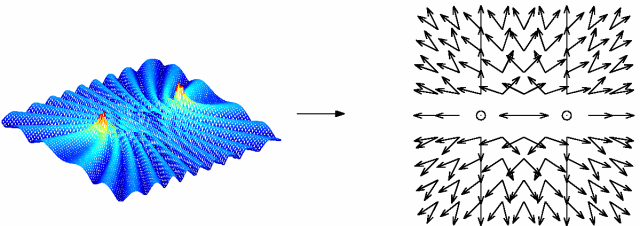
Figure 6: In "Numerical Microlocal Analysis", a numerical solution of Helmholtz (left) is translated into ray representation (right). |
Other projects on high frequency electromagnetics include
a higher order (in frequency)
generalization of physical optics, an efficient method for
finding the creeping ray contribution to
radar cross sections and an
adaptive hp finite element code for
calculating modes in wave guides.
Participants: Björn Engquist, Olof Runborg, Anna-Karin Tornberg, Andreas Atle, Christer Johansson, Mohammad Motamed, KTH, and Erik Abenius, Fredrik Edelvik, Per Lötstedt, Martin Nilsson, Uppsala.
Molecular biology
The key to quantitative descriptions of the dynamic behavior and development of all organisms is understanding the complex networks of feed-back loops that control gene expression. The mathematical models for this are time dependent differential equations. On a macroscopic scale the chemical reactions are governed by ordinary differential equations with time delays. They are very stiff due to the many different time scales in the problem. Partial differential equations will have to be developed for the spatial variation in the cell.
At Uppsala University there is a group at the
Department of Molecular Biology (ICM)
working on the mathematical modeling of the network
of control circuits allowing bacteria
to grow fast and to adapt to changing environment. The
group
is led by professor Måns Ehrenberg.
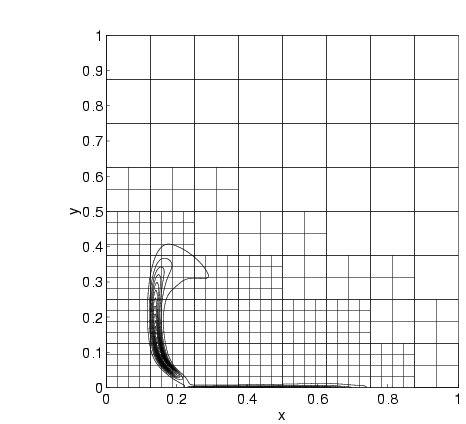 Figure 7 |
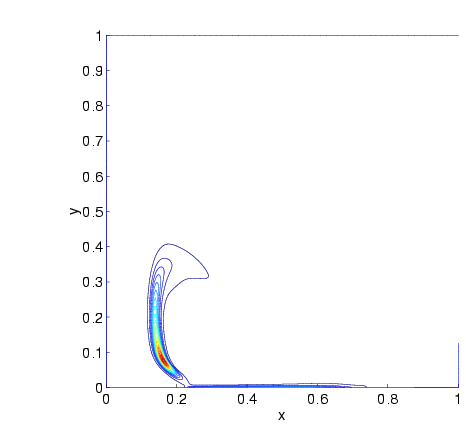 Figure 8 |
| The probability density is computed for a circadian clock modelled with two chemical compounds using an adaptive method. The adapted grid and the steady state solution are displayed in Figure 7 and in Figure 8 the probability is color coded. | |
The number of molecules of each kind is often small. It is estimated that for 80 percent of the proteins in E. coli the number of molecules is less than 100 in a cell. On a mesoscale with few molecules the reactions are described by the master equations. Their solution is a probability density for the combinations of molecules. An example with two molecules is found in Figures 7 and 8. A time-dependent solution is computed with control of the accuracy here. A difficulty with these equations is the high ``spatial'' dimension. The addition of one more molecule in the reactions introduces one more dimension. The standard method of solving these stochastic equations is Monte Carlo simulation. An alternative without the disadvantages of Monte Carlo is to solve approximations of the master equations such as the Fokker-Planck equation.
An adaptive method for low-dimensional problems is described in a recent
report.
New numerical methods are needed to solve these equations on parallel computers
for a quantitative comparison with experimental data and predictions of
cell behavior. Such methods are now under devepoment using various simplifying
assumptions.
There is no plan for the moment to also include the microscale
with simulation of separate molecules.
Participants: Björn Engquist, Olof Runborg, KTH, and Johan Elf, Måns Ehrenberg, Stefan Engblom, Lars Ferm, Per Lötstedt, Paul Sjöberg, Uppsala.
Materials science
Atomistic simulations using molecular dynamics (MD) are playing an increasingly prominent role in a wide area of research which includes material science, condensed matter physics, and structural chemistry. The molecular dynamics simulations make possible to directly monitor the dynamics of individual atoms, thereby providing a unique microscopic insight into the material behaviour that cannot be obtained from laboratory experiments. It has proved to be immensely useful for predicting the properties and performance of new materials which is central to the success of many industrially relevant research projects.
Presently, the molecular dynamics
and related simulation methods consume a major share of the existing
supercomputing resources. Consequently, the development and adequate
implementation of efficient and accurate simulation algorithms, in
particular, exploiting the parallel processing, is a problem of
profound importance. A strategic task of the molecular dynamics
group at NADA is creation and development of a pool of expertise
and a refined methodology that can be exploited by other researchers.
We are particularly interested in coupling the
microscale simulations with the macroscale.
In this context we focus on computer algorithms for the simulation of
epitaxial growth. It is a problem
of practical importance for the production of thin
films in the semiconductor industry. The purpose of these simulations is
the understanding and control of the nanoscale morphology of barrier
layers in quantum devices.
A hierarchy of models is required in order to capture the different scales
in the problem. Ab initio calculation of activation energies is the basis
for kinetic Monte Carlo techniques. The kinetic simulations calibrate
the coefficients in the partial differential equation for the continuum
model for larger scales. Multigrid methods will then be used
to bridge the difference between scales in the continuum model.
Another direction in this project is modeling of oxide reduction under
sintering of P/M components. A reaction-transport model for reduction
of surface oxides in P/M components of Astalloy CrM has been developed
and compared with experiments. A new conductivity model based on
homogenization theory has been developed. This model has fewer free
parameters than the standard models and is more suitable for identification.
The work is done in collaboration
with Höganäs AB, BRIIE and Korrosions- och
Metallforskningsinstitutet AB (KIMAB).
Participants: Björn Engquist, Mikhail Dzugutov, Jesper Oppelstrup, Anna-Karin Tornberg, Erik Sundelöf, KTH
Multiscale methods
This is a supporting project on multiscale analysis and methodology that is general and not applicable only to a particular application.
The focus is on the heterogeneous multiscale method and
"coarse timestepper" based
methods.
The basic premise of this class of methods
is a known, but computationally expensive, microscopic
description of a problem.
The methods assume there exists a simplified macroscopic
description but it is unknown or the knowledge of it is incomplete.
Without explicitly deriving an
intermediate description (neither continuous nor discrete) the macroscale behavior
is computed using the known microscale description directly;
the macroscale quantities are
evolved based on a number of microscale solutions, local in time and space
to gain efficieny.
The work so far has primarily been to formulate the methods in a
general framework, but applications to ODEs, elliptic equations
with small scale material variations, complex discrete systems and interfacial
dynamics have specifically been considered.
In addition, new techniques have been developed for the numerical
approximation of singular functions in PDEs, e.g. delta functions
and characteristic functions.
Participants: Björn Engquist, Olof Runborg, Anna-Karin Tornberg KTH