Här följer en kort historik kring mätning av ljusets hastighet. En längre historia
med mera fakta (fast på engelska) finns här:
The Speed of Light. Sedan finns en beskrivning av det experiment som
gjordes under Upptäckarveckan 1999.
- Historien om ljustes hastighet
- Galileo Galilei (1564-1642)
- Ole Römer
- Moderna metoder att mäta ljushastigheten
- Historen närmar sig slutet
- Sommarlägrets ljushastighetslaboration
- Uppställning
- Kort beskrivning
- Tiden det tar för ljuset att gå från R till M och tillbaka
- Hur mycket har spegeln R roterat?
- Om speglar och reflektion
- Vad blir ljusets hastighet?
- Vad användes linserna till?
Galilei var en italiensk vetenskapsman som intresserade sig
för en hel massa saker. Mest är han känd som teleskopets uppfinnare.
När det gäller teleskopet och kikaren är man inte lika säker
på att Galilei var ensam uppfinnare, det ryktas att det fanns en
holländare som hade liknande ideer. Säkert är i alla fall att kikaren
blev en succe, då man kunde se saker som lågt mycket långt borta. Galilei
var också den första att vända kikaren mot rymden och studera
månar och planeter.
Galilei är den person som får börja historien om ljusets hastighet.
Han föreslog det första sättet att mäta ljusets hastiget. Det var nog inte
många som ens hade funderat över att ljuset kanske har en hastighet och
inte går oändligt fort (även om några av de gamla grekerna naturligvis tänkte
i de banorna...). Galileis experiment bestod i att två personer
med varsin lampa går upp på varsin bergstopp. Först tänder den ena personen
sin lampa. När den andra personen ser ljuset från den första lampan
tänder han sin lampa. När den första personen ser ljuset från den andra
lampan så har det gått en liten stund sedan han tände sin lampa.
Först måste ljuset gå från det första berget till det andra, och sedan
tillbaka igen innan den första personen kan se ljuset från den andra personens
lampa. Detta experiment misslyckades dock, för ljuset går så fort att
Galilei aldirg hann mäta någon tidsskillnad.
Mera om Galilei
Ole Römer var en dansk som studerade Jupiters månar. Jupiter är
den största planeten i solsystemet och den har fyra månar som kan ses med
ett litet teleskop, vilket var allt som fanns på Römers tid. Ibland så blir
månarna förmörkade då de går in bakom Jupiter. Det som Ole Römer
upptäckte var att dessa förmörkelser ibland kom tidigare och ibland senare
än de borde göra. Han drog slutsatsen att detta berodde på att ljusets
hastighet inte var oändlig.
När Juptiermånen i bilden försviner in bakom Juptier börkar det sista
ljuset röra sig mot Jorden. Precis när månen kommer fram igen börjar ljus
återigen sändas iväg mot Jorden. Eftersom Jorden har rört sig en bit i sin bana
(mer än Jupiter har i sin bana) så har detta ljus en längre sträcka att färdas
än det sista ljus som sändes iväg före förmörkelsen. Därför der det
från Jorden ut som om förmörkelsen har varat längre än den egentligen har.
Römer visste hur länge månen borde vara förmörkad, och när han såg att
den var förmörkad längre än så antog han att det berodde på att ljuset
inte har en oändlig hastighet.
Han fick ett värde på ljushastigehten som var cirka 200 000 km/s, vilket
måste anses som mycket bra med tankte på de instrument som fanns att
tillgå på 1600-talet.
Nästa stora framsteg i historien gjordes av Foucault som kom på ett nytt
och mycket bättre sätt att mäta ljushastigheten. Två bergstoppar måste man
ha. På den ena sätter man en spegel och på den andra en lampa som får
lysa genom ett kugghjul som snurrar. När ett gap i kugghjulet passerar framför
lampan så släpps ljus ignom. Detta ljus fortsätter till den andra
bergstoppen och reflekteras mos spegeln. Så småningom kommer det tillbaka
och då står man och tittar bakom kugghjulet. Om man snurrar kugghjulet
lagom fort så kommer kugghjulet att ha snurrat så mycket att en tand kommer
ivägen för det ljus som kommer tillbaka från spegeln, och detta ljus kommer
aldrig fram till observatören. Hur fort kugghjulet måste snurra beror på
hur lång tid det tar för ljuset att gå fram och tillbaka till det andra
berget, vilket i sin tur beror på hur fort ljuset går.
Genom att hålla reda på hur fort kugghjulet snurrar kan man mäta vid
vilket varvtal som ljuset från den andra spegeln inte syns. Sedan kan ljusets
hastighet beräknas.
Michelson utvecklade ljushastighetsmätningen till sin spets och i början av
1900-talet gjorde han de bästa mätningarna någonsin. På sommarlägrets
laboration användes inte ett roterande kugghjul utan istället en roterande
spegel. Med en mycket snabb motor går det att få ner det utrymme
som krävs till ett tiotals meter istället för åtskilliga kilometer.
En bild på laborationsutrustningen
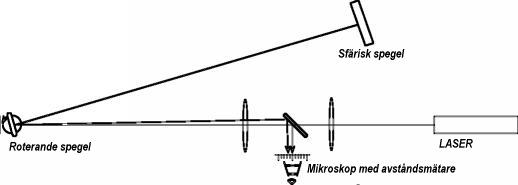
Klicka på bilden för att se en förstoring
En närmare förklaring finns nedan.
För laborationen användes en sfärisk spegel, en roterande spegel, en laser,
två linser och ett mikroskop för mätning av små avstånd. Nedan följer
en kort beskrivning av hur det fungerar och sedan en längre förklaring
till hur själva uträkningarna går till. Uträkningarna görs på en enklare
modell utan linser och mikroskop. Sist beskrivs anledningen till
varför linserna och mikroskopet användes i sommarkursens laboration.
Bild på en förenklad laborationsuppställning
Ljuset från lasern träffar den roterande spegeln R, och reflekteras
mot densfäriska spegeln M. För ljuset tar det en viss tid att gå från
R till M och sedan tillbaka till R. Eftersom R snurrar så har den
roterat en liten vinkel under den tid som det tog för ljuset att gå
fran och tillbaka mellan R och M. Därför kommer ljuset inte att komma
tillbaka i samma riktning, och inte heller träffa mätinstrumentet på
samma ställe som när spegeln R inte snurrar.
Om man rör sig med hastigheten v under en tid t så tillryggalägger
man en sträcka s med längden v*t. Alltså: s = v*t.
Om avståndet mellan speglarna R och M är d, så kommer ljuset att röra sig
en sträcka som är 2*d (fram och tillbaka). Ljushastigheten kallas c och
tiden får vara t. Med formlen ovan blir det 2*d = c*t, vilket ger att
t = 2*d/c.
Om R snurrar med w varv per sekund, och det tar ljuset tiden t att gå fram
och tillbaka mellan R och M, så har R snurrat w*t varv under den tiden.
Varv är ingen praktisk enhet att mäta vinklar i. Grader som används
på kompasser är inte heller så bra just i matematiska sammanhang. Istället
brukar enheten radianer användas. 2*pi radianer är ett varv eller 360 grader.
2*pi är ungefär 6,28.
Om R roterar med w varv per sekund betyder det att R snurrar 2*pi*w
radianer per sekund. En sammanfattning av formlerna hittills ger att
på den tid som det tar för ljuset att gå fram och tillbaka mellan speglarna
R och M så har spegeln R roterat w*t varv = 2*pi*w*t radianer
= 2*pi*w*2*d/c.
Ljus som reflekteras från en spegel har samma vinkel till normalen
som det infallande ljuset.
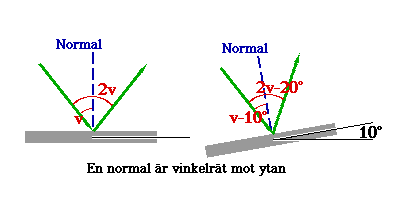I figuren ser man att om spegeln roteras en vinkel r så kommer det reflekterade
ljuset att ändra sin vinkel med 2*r.
I bilden som visar laborationsuppställningen så ser man att det som bestämmer
h (vilken är den sträcka som kan mätas) är vinkeln u.
Vi vet sedan tidigare att den vinkel som spegeln R roterar medan ljuset
går fram och tillbaka mellan R och M är r = 2*pi*w*2*d/c radianer =
4*pi*w*d/c radianer. Vinkeln u blir då 2*r enligt figuren ovan.
Den sträcka som mäts upp, h, beror på avståndet mellan mätinstrumentet och
den roterande spegeln, L. Om vinkeln u är liten och given i radianer, vilket den
är i det här fallet, så kan detta beroende skrivas som h = u*L.
Om allting sammafattas fås h = u*L = 2*r*L = 2*4*pi*w*d*L/c = 8*pi*w*d*L/c.
Denna formel kan skrivas om till c = 8*pi*w*d*L/h.
I förklaringen ovan har linserna inte tagits med. Linserna som användes
i den riktiga laborationen var till för att fokusera laserstrålen så
att den punkt som syntes i mikroskopet skulle bli så liten som möjligt.
När ljus går genom linser så bryts det, det vill säga att det ändrar
riktning. Dessa riktningsändringar måste man ta hänsyn till när man
beräknar längden på sträckan h. Det är anledningen till att formeln
som användes under laborationen på sommarlägret var mer komlicerad än den
som beräknats ovan. Mikroskopet och används för att det ska vara lättare
att mäte de små avståndsskillnadera och den halvgenomskinliga spegeln
finns för att mikroskopet inte ska vara ivägen från strålen från lasern.
