



Next: MINIMUM DOMINATING SET
Up: Covering and Partitioning
Previous: Covering and Partitioning
Index
- INSTANCE:
Graph
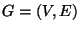 .
.
- SOLUTION:
A vertex cover for G, i.e., a subset
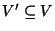 such that, for each
edge
such that, for each
edge 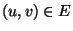 ,
at least one of u and v belongs to V'.
,
at least one of u and v belongs to V'.
- MEASURE:
Cardinality of the vertex cover, i.e.,
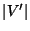 .
.
- Good News:
Approximable within
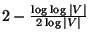 [380] and [62] and
[380] and [62] and
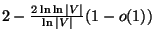 [232].
[232].
- Bad News:
Not approximable within 1.1666 [242].
- Comment:
The good news hold also for the weighted version
[62,232], in which each vertex has a nonnegative
weight and the objective is to minimize the total weight of the vertex
cover. Admits a PTAS for planar graphs [53]
and for unit disk graphs [264], even in the
weighted case.
The case when degrees are bounded by
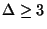 is APX-complete [393] and [9],
for
is APX-complete [393] and [9],
for 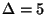 not approximable within 1.0029 [76],
and not
approximable within 1.1666 for a sufficiently large
not approximable within 1.0029 [76],
and not
approximable within 1.1666 for a sufficiently large 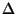 [118]. For
[118]. For 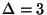 it is
approximable within 7/6 [75], and for general
it is
approximable within 7/6 [75], and for general 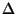 within
within
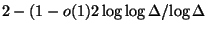 [232].
Approximable within 3/2 for 6-claw-free graphs
(where no independent set of size 6 exists in any neighbour set to any
vertex) [222], and within
[232].
Approximable within 3/2 for 6-claw-free graphs
(where no independent set of size 6 exists in any neighbour set to any
vertex) [222], and within
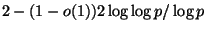 for p+1-claw-free graphs [232].
Variation in which
for p+1-claw-free graphs [232].
Variation in which
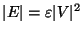 is APX-complete [118], and is approximable within
is APX-complete [118], and is approximable within
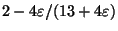 [382].
Approximable within
[382].
Approximable within
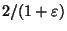 if every vertex has degree at least
if every vertex has degree at least
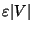 [297] and [294].
When generalized to k-uniform hypergraphs, the problem is equivalent
to MINIMUM SET COVER with fixed number k of occurrences of
each elements. Approximable within
[297] and [294].
When generalized to k-uniform hypergraphs, the problem is equivalent
to MINIMUM SET COVER with fixed number k of occurrences of
each elements. Approximable within
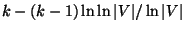 and
and
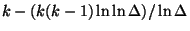 ,
for large values of n and
,
for large values of n and 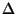 [232].
If the vertex cover is required to induce a connected graph,
the problem is approximable within 2 [429].
If the graph is edge-weighted, the solution is a closed walk whose vertices
form a vertex cover, and the objective is to minimize the sum of the edges
in the cycle, the problem is approximable within 5.5
[27].
The constrained variation in which the input is extended with a positive
integer k and a subset S of V, and the problem is to find the vertex
cover of size k that contains the largest number of vertices from S,
is not approximable within
[232].
If the vertex cover is required to induce a connected graph,
the problem is approximable within 2 [429].
If the graph is edge-weighted, the solution is a closed walk whose vertices
form a vertex cover, and the objective is to minimize the sum of the edges
in the cycle, the problem is approximable within 5.5
[27].
The constrained variation in which the input is extended with a positive
integer k and a subset S of V, and the problem is to find the vertex
cover of size k that contains the largest number of vertices from S,
is not approximable within
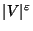 for some
for some
 [476].
The maximization variation in which the input is extended just with a
positive integer k, and the problem is to find k vertices that cover
as many edges as possible, is 2-approximable [92] and
does not admit a PTAS [400].
[476].
The maximization variation in which the input is extended just with a
positive integer k, and the problem is to find k vertices that cover
as many edges as possible, is 2-approximable [92] and
does not admit a PTAS [400].
- Garey and Johnson: GT1




Next: MINIMUM DOMINATING SET
Up: Covering and Partitioning
Previous: Covering and Partitioning
Index
Viggo Kann
2000-03-20