MINIMUM BICONNECTIVITY AUGMENTATION

• INSTANCE: Graph 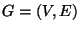$G=\left(V,E\right)$ and a symmetric weight function $w:V \times V \rightarrow N$.

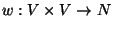• SOLUTION: A connectivity augmenting set E' for G, i.e., a set E' of unordered pairs of vertices from V such that 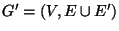$G'=\left(V,E \cup E'\right)$ is biconnected.

• MEASURE: The weight of the augmenting set, i.e., $\sum_{(u,v) \in E'}w(u,v)$.

  
  

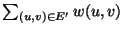• Good News: Approximable within 2 [172] and [319].

• Comment: The same bound is valid also when G' must be bridge connected (edge connected) [319]. Minimum k-Connectivity Augmentation, the problem in which G' has to be k-connected (vertex or edge connected), is also approximable within 2 [310]. If the weight function satisfies the triangle inequality, the problem is approximable within 3/2 [173]. Variation in which G is planar and the augmentation must be planar is approximable within 5/3 in the unweighted case (where w(u,v)=1) [166]. If 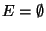$E=\emptyset$ the problem is the same as weighted MINIMUM K-VERTEX CONNECTED SUBGRAPH.

• Garey and Johnson: ND18