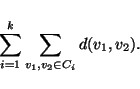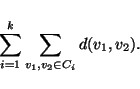Next: MINIMUM K-SUPPLIER
Up: Miscellaneous
Previous: MINIMUM K-CLUSTERING
Index
- INSTANCE:
Finite set X, a distance
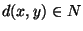 for each pair
for each pair 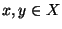 .
The distances must satisfy the triangle inequality.
.
The distances must satisfy the triangle inequality.
- SOLUTION:
A partition of X into disjoint subsets
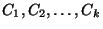 .
.
- MEASURE:
The sum of all distances between elements in the same subset, i.e.,
- Good News:
Approximable within 2 [213].
- Comment:
If the triangle inequality is not satisfied the problem is called
MINIMUM EDGE DELETION
K-PARTITION.
Approximable within 1.7 for k=2 [213].
The maximization variation in which the subsets
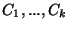 must be
of equal size c is approximable within 2(c-1)/c or (c+1)/c,
depending on whether c is even or odd [160]
Moreover, if d does not satisfy the triangle inequality then the bounds are
c-1 and c, respectively [160];
the cases c=3 and c=4 are approximable within 2 [159].
Finally, if
required sizes
must be
of equal size c is approximable within 2(c-1)/c or (c+1)/c,
depending on whether c is even or odd [160]
Moreover, if d does not satisfy the triangle inequality then the bounds are
c-1 and c, respectively [160];
the cases c=3 and c=4 are approximable within 2 [159].
Finally, if
required sizes 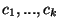 of the subsets are given and the triangle
inequality is satisfied then the maximization problem is approximable
within
of the subsets are given and the triangle
inequality is satisfied then the maximization problem is approximable
within 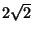 [239].
[239].




Next: MINIMUM K-SUPPLIER
Up: Miscellaneous
Previous: MINIMUM K-CLUSTERING
Index
Viggo Kann
2000-03-20