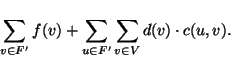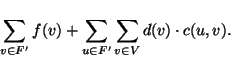Next: MAXIMUM K-FACILITY LOCATION
Up: Miscellaneous
Previous: MAXIMUM K-FACILITY DISPERSION
Index
- INSTANCE:
Complete graph
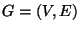 ,
costs
,
costs
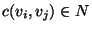 that are
symmetric and satisfy the triangle inequality,
that are
symmetric and satisfy the triangle inequality,
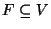 set of
locations where a facility may be built,
for each
set of
locations where a facility may be built,
for each 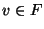 a nonnegative cost f(v) of building a facility at v,
for each location
a nonnegative cost f(v) of building a facility at v,
for each location 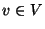 a nonnegative demand d(v).
a nonnegative demand d(v).
- SOLUTION:
Locations for the facilities to be built, i.e.,
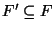 .
.
- MEASURE:
- Good News:
Approximable within 2.408 [209].
- Bad News:
APX-complete [209].
- Comment:
Transformation from MINIMUM VERTEX COVER in bounded degree graphs.
Not approximable within 1.463 unless NP
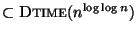 .
If f(v)=1 for every
.
If f(v)=1 for every 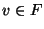 the same hardness results are valid, but
the problem is approximable within 2.225.
If F=V and f(v)=1 then the problem is approximable within 2.104 but
not within 1.278 unless NP
the same hardness results are valid, but
the problem is approximable within 2.225.
If F=V and f(v)=1 then the problem is approximable within 2.104 but
not within 1.278 unless NP
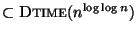 [209].
The generalization to unrestricted cost functions c is approximable
within
[209].
The generalization to unrestricted cost functions c is approximable
within 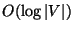 [247].
[247].
Viggo Kann
2000-03-20