



Next: MAXIMUM SET PACKING
Up: Covering, Hitting, and Splitting
Previous: Covering, Hitting, and Splitting
Index
- INSTANCE:
Set
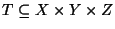 ,
where X, Y, and Z are disjoint.
,
where X, Y, and Z are disjoint.
- SOLUTION:
A matching for T, i.e., a subset
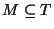 such that no elements
in M agree in any coordinate.
such that no elements
in M agree in any coordinate.
- MEASURE:
Cardinality of the matching, i.e.,
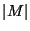 .
.
- Good News:
Approximable within 3/2
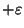 for any
for any
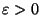 [265].
[265].
- Bad News:
APX-complete [280].
- Comment:
Transformation from MAXIMUM 3-SATISFIABILITY.
In the weighted case, the problem is approximable within
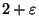 for any
for any
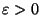 [30].
Admits a PTAS for `planar' instances [386].
Variation in which the number of occurrences of any element in X, Y or
Z is bounded by a constant B is APX-complete for
[30].
Admits a PTAS for `planar' instances [386].
Variation in which the number of occurrences of any element in X, Y or
Z is bounded by a constant B is APX-complete for 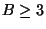 [280].
The generalized Maximum k-Dimensional Matching problem is
approximable within
[280].
The generalized Maximum k-Dimensional Matching problem is
approximable within
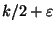 for any
for any
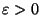 [265], and within 2(k+1)/3 in the weighted case.
The constrained variation in which the input is extended with a subset
S of T, and the problem is to find the 3-dimensional matching
that contains the largest number of elements from S,
is not approximable within
[265], and within 2(k+1)/3 in the weighted case.
The constrained variation in which the input is extended with a subset
S of T, and the problem is to find the 3-dimensional matching
that contains the largest number of elements from S,
is not approximable within
 for some
for some
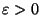 [476].
[476].
- Garey and Johnson: SP1




Next: MAXIMUM SET PACKING
Up: Covering, Hitting, and Splitting
Previous: Covering, Hitting, and Splitting
Index
Viggo Kann
2000-03-20