



Next: MINIMUM COLOR SUM
Up: Covering and Partitioning
Previous: MINIMUM INDEPENDENT DOMINATING SET
Index
- INSTANCE:
Graph
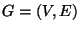 .
.
- SOLUTION:
A coloring of G, i.e., a partition of V into disjoint sets
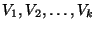 such that each
such that each 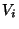 is an independent set for G.
is an independent set for G.
- MEASURE:
Cardinality of the coloring, i.e., the number of disjoint independent sets
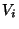 .
.
- Good News:
Approximable within
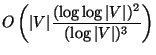 [219].
[219].
- Bad News:
Not approximable within
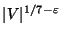 for any
for any
 [68].
[68].
- Comment:
Also called Minimum Chromatic Number.
Not approximable within
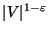 for any
for any
 ,
unless ZPP=NP [156].
If the graph is 3-colorable, the problem is approximable within
,
unless ZPP=NP [156].
If the graph is 3-colorable, the problem is approximable within
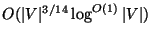 [85],
but not approximable within
[85],
but not approximable within
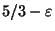 [303].
If the graph is k-colorable the problem is approximable within
[303].
If the graph is k-colorable the problem is approximable within
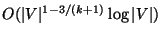 [290].
Approximable with an absolute error guarantee of 1 on planar graphs
by the Four Color Theorem.
Approximable within 3 but not within 1.33 for unit disk graphs
[370].
Approximable within 1+1/e + o(1) on circular arc graphs
[343].
Approximable within
[290].
Approximable with an absolute error guarantee of 1 on planar graphs
by the Four Color Theorem.
Approximable within 3 but not within 1.33 for unit disk graphs
[370].
Approximable within 1+1/e + o(1) on circular arc graphs
[343].
Approximable within
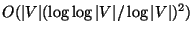 in hypergraphs
[340], and is hard to approximate within
in hypergraphs
[340], and is hard to approximate within
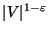 unless NP=ZPP [257,340].
MINIMUM COLORING WITH DEFECT D, the variation where the color
classes
unless NP=ZPP [257,340].
MINIMUM COLORING WITH DEFECT D, the variation where the color
classes 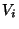 may induce graphs of degree at most d, is not approximable
within
may induce graphs of degree at most d, is not approximable
within
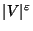 for some
for some
 [123].
MINIMUM FRACTIONAL
CHROMATIC NUMBER, the linear programming relaxation in
which the independent sets
[123].
MINIMUM FRACTIONAL
CHROMATIC NUMBER, the linear programming relaxation in
which the independent sets
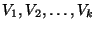 do not need to be
disjoint, and in the solution every independent set
do not need to be
disjoint, and in the solution every independent set 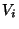 is assigned a
nonnegative value
is assigned a
nonnegative value 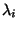 such that for each vertex
such that for each vertex 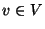 the
sum of the values assigned to the independent sets containing v is
at most 1, and the measure is the sum
the
sum of the values assigned to the independent sets containing v is
at most 1, and the measure is the sum 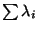 ,
is always within
,
is always within 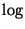 factor from the chromatic number
thus the same bad news apply [365].
The complementary maximization problem, where the number of ``not needed
colors'', i.e.
factor from the chromatic number
thus the same bad news apply [365].
The complementary maximization problem, where the number of ``not needed
colors'', i.e. 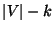 ,
is to be maximized, is approximable
within 360/289 [140].
,
is to be maximized, is approximable
within 360/289 [140].
- Garey and Johnson: GT4




Next: MINIMUM COLOR SUM
Up: Covering and Partitioning
Previous: MINIMUM INDEPENDENT DOMINATING SET
Index
Viggo Kann
2000-03-20
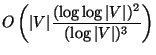 [219].
[219].
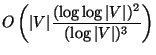 [219].
[219].