



Next: Storage and Retrieval
Up: Weighted Set Problems
Previous: MINIMUM ARRAY PARTITION
Index
- INSTANCE:
An
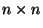 array A of non-negative numbers, positive
integer p.
array A of non-negative numbers, positive
integer p.
- SOLUTION:
A partition of A into p non-overlapping
rectangular subarrays.
- MEASURE:
The maximum weight of any rectangle in the partition. The
weight of a rectangle is the sum of its elements.
- Good News:
Approximable within 2.5 [306].
- Bad News:
Not approximable within 5/4 [306].
- Comment:
The dual problem, where the solution is a tiling where each rectangle has
weight at most p, and the objective is to minimize the number of
rectangles, is approximable within 2.
MAXIMUM RECTANGLE PACKING, the variation in which
l weighted axis-parallel rectangles are given in the input, snd
the objective is to maximize the sum of weights of p disjoint
rectangles is approximable within
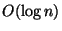 [306].
[306].
Viggo Kann
2000-03-20