



Next: MINIMUM HEIGHT TWO DIMENSIONAL
Up: Data Storage
Previous: Data Storage
Index
- INSTANCE:
Finite set U of items, a size
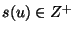 for each
for each 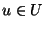 ,
and a
positive integer bin capacity B.
,
and a
positive integer bin capacity B.
- SOLUTION:
A partition of U into disjoint sets
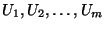 such that
the sum of the items in each
such that
the sum of the items in each 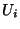 is B or less.
is B or less.
- MEASURE:
The number of used bins, i.e., the number of disjoint sets, m.
- Good News:
Approximable within 3/2 [442] and within
71/60
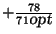 [278], [474].
[278], [474].
- Bad News:
Not approximable within 3/2
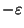 for any
for any
 [182].
[182].
- Comment:
Admits an
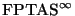 ,
that is, is approximable within
,
that is, is approximable within 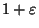 in time
polynomial in
in time
polynomial in 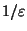 ,
where
,
where
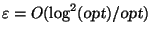 [292].
APX-intermediate unless the polynomial-hierarchy collapses
[125].
A survey of approximation algorithms for MINIMUM BIN PACKING is found in
[120].
If a partial order on U is defined and we require the bin packing to obey
this order, then the problem is approximable within 2
[464], and is not in
[292].
APX-intermediate unless the polynomial-hierarchy collapses
[125].
A survey of approximation algorithms for MINIMUM BIN PACKING is found in
[120].
If a partial order on U is defined and we require the bin packing to obey
this order, then the problem is approximable within 2
[464], and is not in
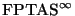 [410].
The generalization in which the cost of a bin is a monotone and concave
function of the number of items in the bin is approximable within
7/4 and is not approximable within 4/3 unless some information about the
cost function is used [24].
The generalization of this problem in which a conflict graph is given
such that adjacent items are assigned to different bins is
approximable within 2.7 for graphs that can be colored in polynomial
time [271] and not approximable within
[410].
The generalization in which the cost of a bin is a monotone and concave
function of the number of items in the bin is approximable within
7/4 and is not approximable within 4/3 unless some information about the
cost function is used [24].
The generalization of this problem in which a conflict graph is given
such that adjacent items are assigned to different bins is
approximable within 2.7 for graphs that can be colored in polynomial
time [271] and not approximable within
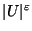 for a given
for a given 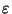 in the general case [365].
in the general case [365].
- Garey and Johnson: SR1




Next: MINIMUM HEIGHT TWO DIMENSIONAL
Up: Data Storage
Previous: Data Storage
Index
Viggo Kann
2000-03-20