



Next: MINIMUM TIME-COST TRADEOFF
Up: Sequencing on One Processor
Previous: MINIMUM PRECEDENCE CONSTRAINED SEQUENCING
Index
- INSTANCE:
Set T of tasks, for each task
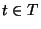 a release time
a release time 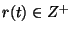 ,
a length
,
a length 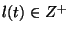 ,
and a weight
,
and a weight 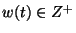 .
.
- SOLUTION:
A one-processor schedule for T that obeys the release times, i.e.
a function
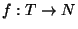 such that, for all
such that, for all 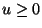 ,
if
S(u) is the set of tasks t for which
,
if
S(u) is the set of tasks t for which
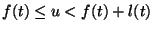 ,
then
,
then 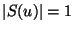 and for each task t,
and for each task t, 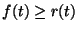 .
.
- MEASURE:
The weighted sum of completion times, i.e.
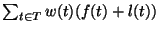 .
.
- Good News:
Approximable within 1.6853 [196].
- Comment:
Approximable within
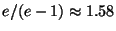 if all weights w(t)=1
[101].
Variation in which there are precedence constraints on T instead of
release times is approximable within 2 [216].
The preemptive case is approximable within 4/3 [431].
Variation in which there are precedence constraints and release times
is approximable within e [433].
If all weights w(t)=1 and the objective is to minimize the max-stretch
if all weights w(t)=1
[101].
Variation in which there are precedence constraints on T instead of
release times is approximable within 2 [216].
The preemptive case is approximable within 4/3 [431].
Variation in which there are precedence constraints and release times
is approximable within e [433].
If all weights w(t)=1 and the objective is to minimize the max-stretch
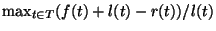 the nonpreemptive problem is not
approximable within
the nonpreemptive problem is not
approximable within
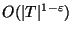 for any
for any
 ,
but the
preemptive problem admits a PTAS [70].
,
but the
preemptive problem admits a PTAS [70].




Next: MINIMUM TIME-COST TRADEOFF
Up: Sequencing on One Processor
Previous: MINIMUM PRECEDENCE CONSTRAINED SEQUENCING
Index
Viggo Kann
2000-03-20