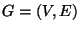SOLUTION:
A coloring of E, i.e., a partition of E into disjoint sets
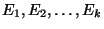such that, for ,
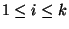no two edges in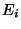
share a common endpoint in G.
MEASURE:
Cardinality of the coloring, i.e., the number of disjoint sets .
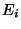Good News:
Approximable within 4/3, and even approximable with an absolute error
guarantee of 1 [461].
Bad News:
Not approximable within 4/3
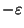for any
[258].
Comment:
Also called Minimum Chromatic Index.
APX-intermediate unless the polynomial-hierarchy collapses
[125].
On multigraphs the problem is approximable within 1.1
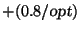[387].
The maximization variation in which the input is extended with a
positive integer k, and the problem is to find the maximum number of
consistent vertices over all edge-colorings with k colors,
is approximable within e/(e-1) [80], but does not admit a PTAS [400].
.
such that, for 
,
no two edges in 
share a common endpoint in G.
for any
[258].
[387].
The maximization variation in which the input is extended with a
positive integer k, and the problem is to find the maximum number of
consistent vertices over all edge-colorings with k colors,
is approximable within e/(e-1) [80], but does not admit a PTAS [400].