



Next: MINIMUM MAXIMAL MATCHING
Up: Covering and Partitioning
Previous: MINIMUM FEEDBACK VERTEX SET
Index
- INSTANCE:
Directed graph
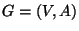 .
.
- SOLUTION:
A feedback arc set, i.e., a subset
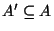 such that A'
contains at least one arc from every directed cycle in G.
such that A'
contains at least one arc from every directed cycle in G.
- MEASURE:
Cardinality of the feedback arc set, i.e.,
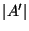 .
.
- Good News:
Approximable within
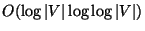 [148].
[148].
- Bad News:
APX-hard [282].
- Comment:
Transformation from MINIMUM FEEDBACK VERTEX SET [148].
The generalized variation in which the input is extended with a subset S
of vertices and arcs, and the problem is to find an arc set that
contains at least one arc from every directed cycle that intersects S,
is approximable within
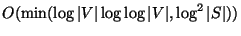 [148].
All these problems are approximable within 9/4 for planar graphs
[199].
The constrained variation in which the input is extended with a positive
integer k and a subset S of A, and the problem is to find the feedback
arc set of size k that contains the largest number of arcs from S,
is not approximable within
[148].
All these problems are approximable within 9/4 for planar graphs
[199].
The constrained variation in which the input is extended with a positive
integer k and a subset S of A, and the problem is to find the feedback
arc set of size k that contains the largest number of arcs from S,
is not approximable within
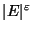 for some
for some
 [476].
The complementary problem of finding the maximum set of arcs A' such that
[476].
The complementary problem of finding the maximum set of arcs A' such that
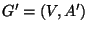 is acyclic is approximable within
is acyclic is approximable within
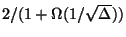 where
where 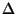 is the maximum degree
[72] and [237], it is APX-complete
[393],
and if
is the maximum degree
[72] and [237], it is APX-complete
[393],
and if
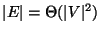 it admits a PTAS [36].
it admits a PTAS [36].
- Garey and Johnson: GT8




Next: MINIMUM MAXIMAL MATCHING
Up: Covering and Partitioning
Previous: MINIMUM FEEDBACK VERTEX SET
Index
Viggo Kann
2000-03-20