



Next: MINIMUM BOTTLENECK PATH MATCHING
Up: Covering and Partitioning
Previous: MAXIMUM TRIANGLE PACKING
Index
- INSTANCE:
Graph
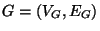 and a fixed graph
and a fixed graph
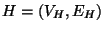 with at least
three vertices in some connected component.
with at least
three vertices in some connected component.
- SOLUTION:
A H-matching for G, i.e., a collection
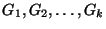 of
disjoint subgraphs of G, each isomorphic to H.
of
disjoint subgraphs of G, each isomorphic to H.
- MEASURE:
Cardinality of the H-matching, i.e., the number of disjoint subgraphs
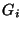 .
.
- Good News:
Approximable within
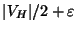 for any
for any
 [265].
[265].
- Bad News:
APX-hard [283].
- Comment:
Also called Maximum H-Packing.
Transformation from bounded MAXIMUM 3-SATISFIABILITY.
The weighted version can be approximated within
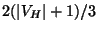 [98].
Variation in which the degree of G is bounded by a constant B is
APX-complete [283].
Admits a PTAS for planar graphs [53],
but does not admit an FPTAS [73].
Admits a PTAS for
[98].
Variation in which the degree of G is bounded by a constant B is
APX-complete [283].
Admits a PTAS for planar graphs [53],
but does not admit an FPTAS [73].
Admits a PTAS for 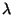 -precision unit disk graphs
[264].
The case when H is the path with three edges is approximable within
4/3, even in the edge-weighted case [238].
Induced MAXIMUM H-MATCHING, i.e., where the subgraphs
-precision unit disk graphs
[264].
The case when H is the path with three edges is approximable within
4/3, even in the edge-weighted case [238].
Induced MAXIMUM H-MATCHING, i.e., where the subgraphs 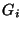 are induced subgraphs
of G, has the same good and bad news as the ordinary problem, even when
the degree of G is bounded.
MAXIMUM MATCHING OF
CONSISTENT K-CLIQUES is the variation in which H is a k-clique
and the vertices of G are partitioned into k independent sets
are induced subgraphs
of G, has the same good and bad news as the ordinary problem, even when
the degree of G is bounded.
MAXIMUM MATCHING OF
CONSISTENT K-CLIQUES is the variation in which H is a k-clique
and the vertices of G are partitioned into k independent sets
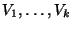 ,
each
,
each 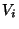 is partitioned into some sets
is partitioned into some sets 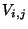 ,
and
at most one vertex in each
,
and
at most one vertex in each 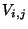 may be included in the matching.
This problem is not in APX for
may be included in the matching.
This problem is not in APX for 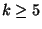 and is not approximable within
4/3 for
and is not approximable within
4/3 for 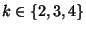 .
It is not in APX for any
.
It is not in APX for any 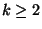 unless
NP
unless
NP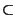 QP [457].
QP [457].
- Garey and Johnson: GT12




Next: MINIMUM BOTTLENECK PATH MATCHING
Up: Covering and Partitioning
Previous: MAXIMUM TRIANGLE PACKING
Index
Viggo Kann
2000-03-20