Comment:
Variation in which the tree is not given as an input and the objective
is to find the tree with the minimum total alignment cost is called
MINIMUM GENERALIZED TREE ALIGNMENT or
MINIMUM EVOLUTIONARY TREE and is APX-hard [273].
The variation of this latter problem which makes use of the quartet paradigm
belongs to PTAS [272].
MINIMUM SEQUENCE ALIGNMENT, the variation in which the objective
is to minimize the sum of edit distances of all pairs of sequences in
the alignment, is approximable within 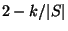 for
any fixed constant
for
any fixed constant 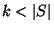 [51].
The generalization of MINIMUM SEQUENCE ALIGNMENT to weighted
sums is approximable within
[51].
The generalization of MINIMUM SEQUENCE ALIGNMENT to weighted
sums is approximable within 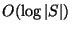 [469].
[469].
![]() for
any fixed constant
for
any fixed constant ![]() [51].
The generalization of MINIMUM SEQUENCE ALIGNMENT to weighted
sums is approximable within
[51].
The generalization of MINIMUM SEQUENCE ALIGNMENT to weighted
sums is approximable within ![]() [469].
[469].