



Next: MAXIMUM BALANCED CONNECTED PARTITION
Up: Covering and Partitioning
Previous: MINIMUM CLIQUE PARTITION
Index
- INSTANCE:
Graph
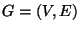 ,
and a weight function
,
and a weight function
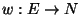 .
.
- SOLUTION:
A k-capacitated tree partition of G, i.e., a collection of vertex disjoint
subsets
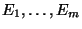 of E such that, for each i, the subgraph induced
by
of E such that, for each i, the subgraph induced
by 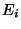 is a tree of at least k vertices.
is a tree of at least k vertices.
- MEASURE:
The weight of the partition, i.e.,
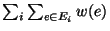 .
.
- Good News:
Approximable within
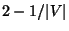 [197].
[197].
- Comment:
The variation in which the trees must contain exactly k vertices and the
triangle inequality is satisfied is approximable within
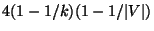 .
Similar results hold for the corresponding cycle and path partitioning problems
with the triangle inequality [197].
Variation in which the trees must contain exactly k vertices and the
objective is to minimize
.
Similar results hold for the corresponding cycle and path partitioning problems
with the triangle inequality [197].
Variation in which the trees must contain exactly k vertices and the
objective is to minimize
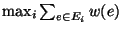 is not in APX,
but if the triangle inequality is satisfied it is approximable within
is not in APX,
but if the triangle inequality is satisfied it is approximable within
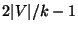 [211].
The variation in which the number m of trees is fixed, the trees'
sizes are exactly specified, and the triangle inequality is satisfied
is approximable within 2p-1 [212].
[211].
The variation in which the number m of trees is fixed, the trees'
sizes are exactly specified, and the triangle inequality is satisfied
is approximable within 2p-1 [212].
Viggo Kann
2000-03-20