



Next: MAXIMUM INDEPENDENT SEQUENCE
Up: Subgraphs and Supergraphs
Previous: MAXIMUM CLIQUE
Index
- INSTANCE:
Graph
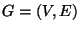 .
.
- SOLUTION:
An independent set of vertices, i.e. a subset
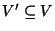 such that
no two vertices in V' are joined by an edge in E.
such that
no two vertices in V' are joined by an edge in E.
- MEASURE:
Cardinality of the independent set, i.e.,
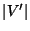 .
.
- Good News:
See MAXIMUM CLIQUE.
- Bad News:
See MAXIMUM CLIQUE.
- Comment:
The same problem as MAXIMUM CLIQUE on the complementary graph.
Admits a PTAS for planar graphs [53]
and for unit disk graphs [264].
The case of degree bounded by
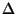 for
for 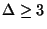 is
is APX-complete [393] and [75],
is not approximable within
is
is APX-complete [393] and [75],
is not approximable within
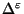 for some
for some
 [12],
and not approximable within 1.0005 for B=3, 1.0018 for
[12],
and not approximable within 1.0005 for B=3, 1.0018 for 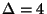 and 1.0030
for
and 1.0030
for 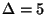 [76].
It is approximable within
[76].
It is approximable within 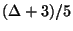 [75] for small
[75] for small 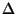 ,
and within
,
and within
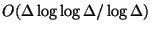 for larger values
[290,14,460].
Also approximable on sparse graphs within
for larger values
[290,14,460].
Also approximable on sparse graphs within
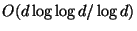 where d is the
average degree of the graph [224].
Approximable within
where d is the
average degree of the graph [224].
Approximable within
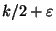 for k+1-claw free graphs
[222].
The vertex weighted version is approximable within
3/2 for
for k+1-claw free graphs
[222].
The vertex weighted version is approximable within
3/2 for 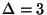 [248], within
[248], within 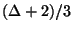 for
for 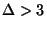 [218], and within
[218], and within
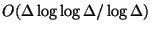 for larger values of
for larger values of 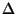 [224].
The related problem in hypergraphs is approximable within
[224].
The related problem in hypergraphs is approximable within
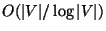 [224], also in the weighted case.
MAXIMUM INDEPENDENT SET OF K-GONS, the variation in which the number of pairwise independent
k-gons (cycles of size k,
[224], also in the weighted case.
MAXIMUM INDEPENDENT SET OF K-GONS, the variation in which the number of pairwise independent
k-gons (cycles of size k, 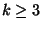 )
is to be maximized
and where two k-gons are independent if any edge connecting
vertices from different k-gons must belong to at least one of these
k-gons, is not approximable within 4/3 for any
)
is to be maximized
and where two k-gons are independent if any edge connecting
vertices from different k-gons must belong to at least one of these
k-gons, is not approximable within 4/3 for any 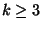 .
It is not in
APX for any
.
It is not in
APX for any 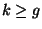 unless NP
unless NP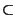 QP [457].
QP [457].
- Garey and Johnson: GT20




Next: MAXIMUM INDEPENDENT SEQUENCE
Up: Subgraphs and Supergraphs
Previous: MAXIMUM CLIQUE
Index
Viggo Kann
2000-03-20