



Next: MINIMUM VERTEX DELETION TO
Up: Subgraphs and Supergraphs
Previous: MAXIMUM INDEPENDENT SEQUENCE
Index
- INSTANCE:
Graph
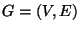 .
The property P must be hereditary, i.e., every subgraph of G' satisfies
P whenever G' satisfies P, and non-trivial, i.e., it is satisfied
for infinitely many graphs and false for infinitely many graphs.
.
The property P must be hereditary, i.e., every subgraph of G' satisfies
P whenever G' satisfies P, and non-trivial, i.e., it is satisfied
for infinitely many graphs and false for infinitely many graphs.
- SOLUTION:
A subset
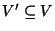 such that the subgraph induced by V' has the
property P.
such that the subgraph induced by V' has the
property P.
- MEASURE:
Cardinality of the induced subgraph, i.e.,
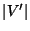 .
.
- Good News:
Approximable within
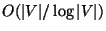 [224].
[224].
- Bad News:
Not approximable within
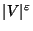 for some
for some
 unless P=NP, if P is false for some clique or independent set (for
example planar, outerplanar, bipartite, complete bipartite, acyclic,
degree-constrained, chordal, interval).
Not approximable within
unless P=NP, if P is false for some clique or independent set (for
example planar, outerplanar, bipartite, complete bipartite, acyclic,
degree-constrained, chordal, interval).
Not approximable within
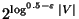 for any
for any
 unless NP
unless NP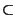 QP, if P is a non-trivial
hereditary graph property (for example comparability, permutation, perfect,
circular-arc, circle, line graph) [364].
QP, if P is a non-trivial
hereditary graph property (for example comparability, permutation, perfect,
circular-arc, circle, line graph) [364].
- Comment:
Approximable within
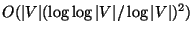 if
P is false for some clique or independent set
[224], and approximable within
if
P is false for some clique or independent set
[224], and approximable within
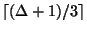 where
where 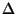 is the maximum degree [218].
All these good news are valid also for the vertex weighted version
[224].
The same problem on directed graphs is not approximable within
is the maximum degree [218].
All these good news are valid also for the vertex weighted version
[224].
The same problem on directed graphs is not approximable within
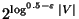 for any
for any
 unless
NP
unless
NP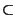 QP, if P is a non-trivial hereditary digraph property
(for example acyclic, transitive, symmetric, antisymmetric, tournament,
degree-constrained, line digraph)
[364].
Admits a PTAS for planar graphs if P is hereditary and determined
by the connected components, i.e., G' satisfies P whenever every
connected component of G' satisfies P
[386].
Admits a PTAS for
QP, if P is a non-trivial hereditary digraph property
(for example acyclic, transitive, symmetric, antisymmetric, tournament,
degree-constrained, line digraph)
[364].
Admits a PTAS for planar graphs if P is hereditary and determined
by the connected components, i.e., G' satisfies P whenever every
connected component of G' satisfies P
[386].
Admits a PTAS for 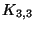 -free or
-free or 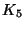 -free graphs if P is hereditary [108].
-free graphs if P is hereditary [108].
- Garey and Johnson: GT21




Next: MINIMUM VERTEX DELETION TO
Up: Subgraphs and Supergraphs
Previous: MAXIMUM INDEPENDENT SEQUENCE
Index
Viggo Kann
2000-03-20