



Next: MINIMUM GRAPH TRANSFORMATION
Up: Iso- and Other Morphisms
Previous: MAXIMUM COMMON INDUCED SUBGRAPH
Index
- INSTANCE:
Trees
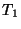 and
and 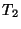 with labels on the nodes.
with labels on the nodes.
- SOLUTION:
A common embedded sub-tree, i.e. a labeled tree T' that can be embedded
into both
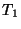 and
and 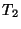 .
An embedding from T' to T is an injective
function from the nodes of T' to the nodes of T that preserves labels
and ancestorship. Note that since fathership does not need to be preserved,
T' does not need to be an ordinary subtree.
.
An embedding from T' to T is an injective
function from the nodes of T' to the nodes of T that preserves labels
and ancestorship. Note that since fathership does not need to be preserved,
T' does not need to be an ordinary subtree.
- MEASURE:
Cardinality of the common embedded sub-tree, i.e.,
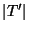 .
.
- Good News:
Approximable within
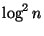 ,
where n is the number of nodes in the trees
[230].
,
where n is the number of nodes in the trees
[230].
- Bad News:
APX-hard
[475].
- Comment:
Transformation from MAXIMUM K-SET PACKING.
Variation in which the problem is to minimize the edit distance between
the two trees is also APX-hard.
Viggo Kann
2000-03-20