



Next: Cuts and Connectivity
Up: Spanning Trees
Previous: MAXIMUM MINIMUM SPANNING TREE
Index
- INSTANCE:
Graph G=(V,E), three edge weight functions
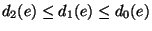 (for each
(for each 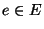 ), where
), where 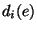 denotes the weight of
edge e if i of its endpoints are ``upgraded'', vertex upgrade
costs c(v) (for each
denotes the weight of
edge e if i of its endpoints are ``upgraded'', vertex upgrade
costs c(v) (for each 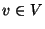 ), a threshold value D for the weight of a
minimum spanning tree.
), a threshold value D for the weight of a
minimum spanning tree.
- SOLUTION:
An upgrading set
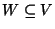 of vertices such that the weight of a minimum
spanning tree in G with respect to edge weights given by
of vertices such that the weight of a minimum
spanning tree in G with respect to edge weights given by 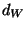 is bounded by D.
Here,
is bounded by D.
Here, 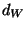 denotes the edge weight function resulting from the upgrade of
the vertices in W, i.e.,
denotes the edge weight function resulting from the upgrade of
the vertices in W, i.e.,
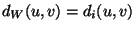 where
where
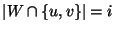 .
.
- MEASURE:
The cost of the upgrading set, i.e.,
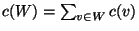 .
.
- Good News:
Approximable within
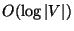 if the difference of the largest edge
weight
if the difference of the largest edge
weight
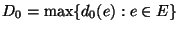 and the smallest edge weight
and the smallest edge weight
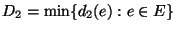 is bounded by a polynomial in
is bounded by a polynomial in 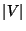 [342].
[342].
- Bad News:
At least as hard to approximate as MINIMUM DOMINATING SET [342].
- Comment: Variation in which the upgrading set must be chosen such that
the upgraded graph contains a spanning tree in which no edge has
weight greater than D is approximable within
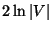 .
In this case
no additional assumptions about the edge weights are necessary. This
variation of the problem is also at least as hard to approximate as
MINIMUM DOMINATING SET [342].
.
In this case
no additional assumptions about the edge weights are necessary. This
variation of the problem is also at least as hard to approximate as
MINIMUM DOMINATING SET [342].




Next: Cuts and Connectivity
Up: Spanning Trees
Previous: MAXIMUM MINIMUM SPANNING TREE
Index
Viggo Kann
2000-03-20