Denna tjänst avvecklas 2026-01-19. Läs mer här (länk)

Denna tjänst avvecklas 2026-01-19. Läs mer här (länk)

MAXIMUM CUT

• INSTANCE: Graph $G=\left(V,E\right)$.

• SOLUTION: A partition of V into disjoint sets $V_1$ and $V_2$.

• MEASURE: The cardinality of the cut, i.e., the number of edges with one end point in $V_1$ and one endpoint in $V_2$.

  
  

• Good News: Approximable within 1.1383 [198].

• Bad News: APX-complete [393].

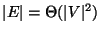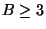• Comment: Not approximable within 1.0624 [242]. Admits a PTAS if $\vert E\vert =\Theta(\vert V\vert^2)$ [39]. Variation in which the degree of G is bounded by a constant B for $B \ge 3$ is still APX-complete [393] and [9]. Variation in which each edge has a nonnegative weight and the objective is to maximize the total weight of the cut is as hard to approximate as the original problem [128] and admits a PTAS for dense instances [162] and for metric weights [164]. Variation in which some pairs of vertices are restricted to be on the same side (or on different sides) is still approximable within 1.138 [198].

  MAXIMUM BISECTION, the weighted problem with the additional constraint that the partition must cut the graph into halves of the same size, is approximable within 1.431 [472]. Admits a PTAS for some classes of weighted dense instances of MAXIMUM BISECTION [162].

  MINIMUM BISECTION, the problem where the partition must cut the graph into halves of the same size and the number of edges between them is to be minimized, admits a PTAS if the degree of each vertex is 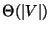$\Theta(\vert V\vert)$ [39].

• Garey and Johnson: ND16