Comment:
The unweighted version is equivalent to MAXIMUM K-COLORABLE SUBGRAPH.
Approximable within 1.21 for k=3, 1.18 for k=4, and 1.15 for k=5
[176].
Not approximable within 1+1/(34k)
[286].
MAXIMUM K-SECTION, the problem with the additional constraint
that the partition must cut the graph into sets of equal size, is
approximable within
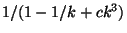 for some constant c>0
[19].
for some constant c>0
[19].
The constrained variation in which the input is extended with a positive
integer W, a vertex 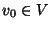 and a subset S of V, and the problem
is to find the 2-cut of weight at least W with the largest number of
vertices from S on the same side as
and a subset S of V, and the problem
is to find the 2-cut of weight at least W with the largest number of
vertices from S on the same side as 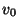 ,
is not approximable within
,
is not approximable within
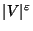 for some
for some
 [476].
[476].
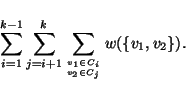
![]() and a subset S of V, and the problem
is to find the 2-cut of weight at least W with the largest number of
vertices from S on the same side as
and a subset S of V, and the problem
is to find the 2-cut of weight at least W with the largest number of
vertices from S on the same side as ![]() ,
is not approximable within
,
is not approximable within
![]() for some
for some
![]() [476].
[476].