| Topology-based Smoothing of 2D Scalar Fields with C1-Continuity | Corresponding Publication | |
 |
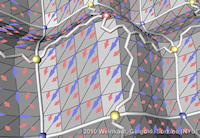
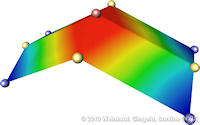
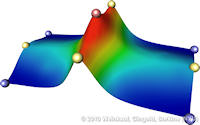
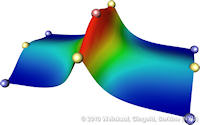
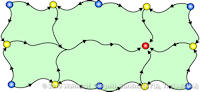
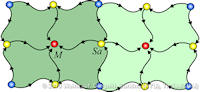
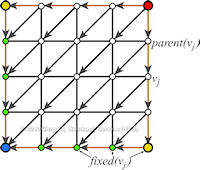
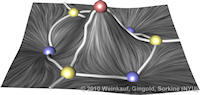
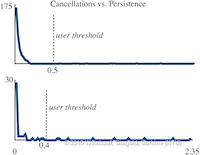
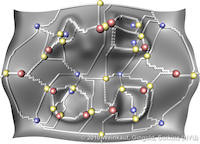
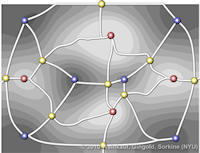
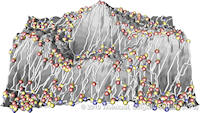
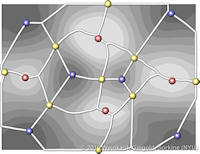
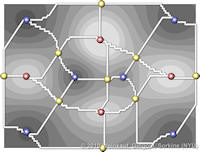
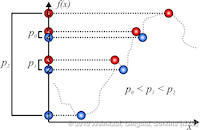
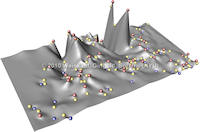
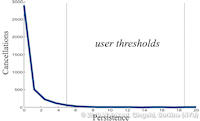
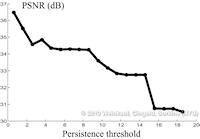
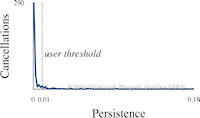
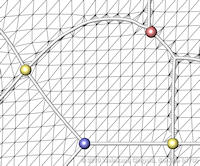
Data sets coming from simulations or sampling of real-world phenomena often contain noise that hinders their processing and analysis. Automatic filtering and denoising can be challenging: when the nature of the noise is unknown, it is difficult to distinguish between noise and actual data features; in addition, the filtering process itself may introduce artificial features into the data set that were not originally present. In this paper, we propose a smoothing method for 2D scalar fields that gives the user explicit control over the data features. We define features as critical points of the given scalar function, and the topological structure they induce (i.e., the Morse-Smale complex). Feature significance is rated according to topological persistence. Our method allows filtering out spurious features that arise due to noise by means of topological simplification, providing the user with a simple interface that defines the significance threshold, coupled with immediate visual feedback of the remaining data features. In contrast to previous work, our smoothing method guarantees a C1-continuous output scalar field with the exact specified features and topological structures. | Topology-based Smoothing of 2D Scalar Fields with C1-Continuity Computer Graphics Forum (Proc. EuroVis) 29(3), June 2010 |
| [slideshow] | ||