| Stable Feature Flow Fields | Corresponding Publication | |
 |
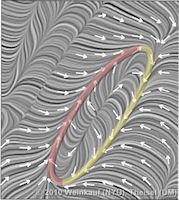
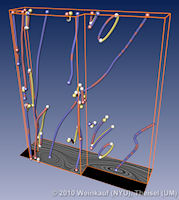
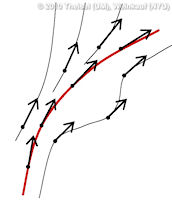
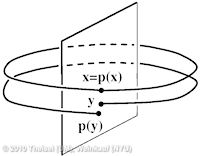
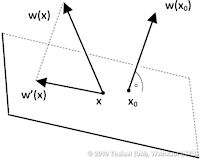
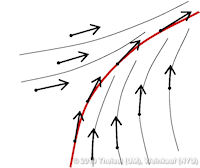
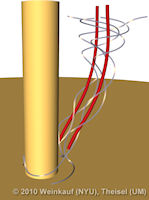
Feature Flow Fields are a well-accepted approach for extracting and tracking features. In particular, they are often used to track critical points in time-dependent vector fields and to extract and track vortex core lines. The general idea is to extract the feature or its temporal evolution using a stream line integration in a derived vector field - the so-called Feature Flow Field (FFF). Hence, the desired feature line is a stream line of the FFF. As we will carefully analyze in this paper, the stream lines around this feature line may diverge from it. This creates an unstable situation: if the integration moves slightly off the feature line due to numerical errors, then it will be captured by the diverging neighborhood and carried away from the real feature line. The goal of this paper is to define a new FFF with the guarantee that the neighborhood of a feature line has always converging behavior. This way, we have an automatic correction of numerical errors: if the integration moves slightly off the feature line, it automatically moves back to it during the ongoing integration. This yields results which are an order of magnitude more accurate than the results from previous schemes. We present new stable FFF formulations for the main applications of tracking critical points and solving the Parallel Vectors operator. We apply our method to a number of data sets. | Stable Feature Flow Fields IEEE Transactions on Visualization and Computer Graphics 17(6), June 2011 |
| [slideshow] | ||