Fördelen med att se ett problem som ett grafproblem är att man lätt ser kopplingen till andra problem som man kanske vet lösningen till. Typiska grafproblem är t.ex.
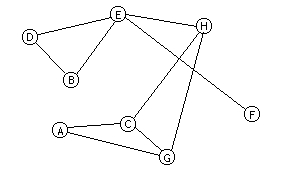
I figuren nedan ges ett exempel på en graf. En graf består av ett antal noder (engelska: vertex - vertices) (i figuren markerade med bokstäver) och ett antal bågar (engelska: edges) som sammanbinder vissa par av noder. Grafer uppträder mycket ofta både i tävlingsproblem och i verkliga livet. T.ex. kan noderna vara datorer i ett nätverk eller städer förbundna med landsvägar, men de kan också representera möjliga ställningar i ett spel med bågarna som möjliga drag. Det viktiga med en graf är att hur den ritas geometriskt (vinklar och längder) är ointressant, endast hur bågarna kopplar samman noderna spelar någon roll.

Fördelen med att se ett problem som ett grafproblem är att man
lätt ser kopplingen till andra problem som man kanske vet lösningen
till. Typiska grafproblem är t.ex.
| Term | Förklaring |
| enkel graf | Det finns inga bågar som går från en nod till sig själv. Detta förutsätts hädanefter. |
| oriktad graf | Bågarna har ingen speciell riktning utan kopplar helt enkelt ihop två noder. |
| riktad graf | Bågarna pekar i en viss riktning, vilket markeras med pilar. Ibland kan det finnas pilar både A->B och B->A, men detta räknas som två bågar. |
| väg (path) | Ett sätt att gå mellan två noder genom att följa bågarna från nod till nod. Samma båge får inte användas två gånger. I en riktad graf får man bara gå i pilens riktning. |
| viktad graf | Varje båge förses med ett tal, som t.ex. anger hur lång sträcka som motsvaras av bågen eller hur mycket av något som kan passera genom bågen samtidigt. |
| sammanhängande graf | Alla noder hänger samman. I figuren ovan är grafen sammanhängande, men om bågen mellan E och H tas bort är den inte sammanhängande längre. I en sammanhängande oriktad graf finns det en väg mellan vilket par av noder som helst, men detta behöver inte gälla för en riktad graf. |
| sammanhängande komponenter | De sammanhängande delarna av en osammanhängande graf. Om t.ex. EH-bågen togs bort i grafen ovan skulle grafen bestå av två sammanhängande komponenter: DBEF och HCAG |
| komplett graf | En oriktad graf där det finns en båge mellan varje par av noder. |
| grad (degree) | Ett tal för varje nod som anger hur många andra noder den har bågar till. För riktade grafer används in-degree och out-degree. |
| cykel | En väg som kommer tillbaka till samma nod som den startade från. För en oriktad graf förutsätts också att s |
| acyklisk graf | En graf som inte innehåller någon cykel. |
| träd | En oriktad, sammanhängande och acyklisk graf. |
Längst ner på den här sidan finns några teorifrågor med svar som kanske kan underlätta förståelsen av termerna.
Representation av grafer
I en dator kan naturligtvis inte en graf representeras grafiskt, utan den måste som vanligt beskrivas med hjälp av information lagrad i någon datastruktur. Vilken struktur man väljer under en tävling beror på
Det finns två vanliga sätt att lagra grafer.
1. Adjacency-list representation
För varje nod u sparas en lista med de noder som u
har bågar till. Det elegantaste är att använda länkade
listor, särskilt om noderna förväntas ha mycket varierande
grad. Men nästan alltid räcker minnet till att använda en
tvådimensionell n*n-matris
(n = antalet noder i grafen), man vet ju att graden för en nod
inte kan överstiga n. Om grafen är viktad måste man
för varje nod också ha en lista med "vikten" till motsvarande
båge.
Listrepresentation är att föredra för de flesta algoritmer,
särskilt för glesa grafer, eftersom ingen "luft" byggs in i tabellen.
När man t.ex. vill vandra runt i grafen (BFS eller DFS) och befinner
sig vid nod A är det bara att gå igenom listan för
att se till vilka noder man kan gå till. Observera att i en oriktad
graf förekommer varje båge på två ställen.
Exempel på listrepresentation
|
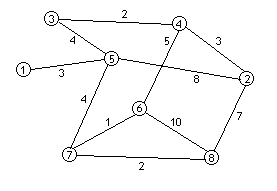
|
2. Adjacency-matrix representation
Grafen lagras som en n*n-matris A där A[u, v] är 1 om det finns en båge från noden u till noden v och 0 om det inte finns någon sådan båge. För en viktad graf låter man istället A[u, v] vara lika med vikten av bågen om det finns någon, annars ett lämpligt default-värde (0 eller "oändligheten").
Matrisrepresentation är ett självklart val när grafen är
komplett, men passar även bra för andra täta grafer. När
man vill vandra omkring i grafen och befinner sig vid noden A går
man igenom A:s rad i matrisen och kollar för varje nod om den
är möjlig att gå till eller inte. Detta är naturligtvis
oekonomiskt för glesa grafer. Matrisrepresentation kan också behövas
vid vissa grafalgoritmer som bygger på matrismultiplikation (se vidare
Kortaste vägen
). Observera att i en oriktad graf är matrisen symmetrisk.
Exempel på matrisrepresentation
|

|
1. Hur många bågar finns det totalt i
a) en komplett graf med 10 noder?
b) ett träd med 10 noder?
c) en oriktad graf med 10 noder som består av tre sammanhängande
komponenter varav en innehåller en cykel?
2. Ange för varje påstående om det ärsant
eller falskt.
a) I en cyklisk, riktad, sammanhängande graf finns det alltid
en väg mellan två noder u och v.
b) I en oriktad graf finns det alltid en väg mellan u och v
om dessa tillhör samma sammanhängande komponent.
c) I ett träd har alla noder samma grad.
d) En cykel i en oriktad graf måste bestå av minst tre bågar.
e) En cykel i en riktad graf måste bestå av minst två
bågar.
f) Summan av graden för alla noder i en oriktad graf är alltid
jämn.
3. På en fest med 10 personer råkar det bli så
att varje person skakar hand med 5 andra. Detta kan beskrivas som en oriktad
graf där personerna är noder och handskakningarna bågar.
a) Vilka av följande egenskaper kan du definitivt veta om grafen?
* sammanhängande / ej sammanhängande
* acyklisk / cyklisk
b) En av personerna hävdar bestämt att han inte skakat hand alls.
Visa att någon ljuger.
c) Om antalet 5 istället vore ett genomsnitt, skulle svaret på
a) då ändras?
4. Visa att för en riktad, acyklisk graf (DAG) kan man placera noderna i en rad från vänster till höger så att alla bågar pekar åt höger. (Topologisk sortering)
Tävlingsuppgifter
Här är några allmänna grafproblem, det finns många
att välja på. Tyvärr har de tre sista ingen automatisk rättning.